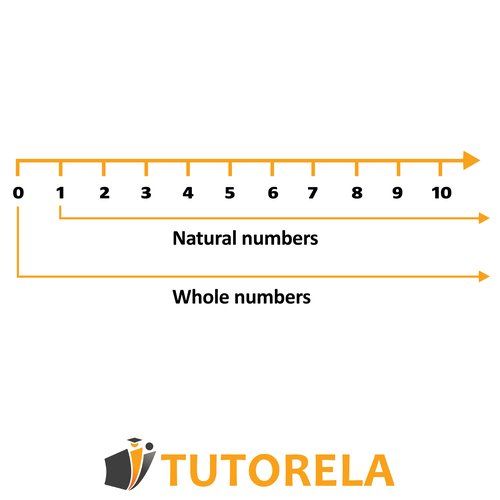
Natural numbers are whole and positive numbers.
To be called a "natural number", it must be whole and positive.
is considered a natural number.
Natural numbers
Natural Numbers
What is a natural number?
Examples of natural numbers

Natural Numbers
In this article, you will learn everything you need to know about natural numbers and you will put it into practice in various exercises.
Shall we start?
What is a natural number?
A natural number must be whole and positive.
Observe: For a number to be considered natural, it must meet both conditions, be positive and whole.
In everyday life, we use natural numbers all the time, almost every time we have to count or calculate something.
What about ?
is also a natural number.
Natural numbers are infinite: All the positive whole numbers from to infinity are called natural numbers.
With them, we can count anything we want and also add, subtract, multiply, and divide.
And now, what do we do? Let's practice!
Find the natural numbers within the following set
Solution:
According to its definition, a natural number is a whole and positive number. Therefore:
: Natural number –> whole and positive.
: Natural number –> is included within the set of natural numbers.
: Number that is not natural –> it is negative (does not meet the condition of being positive)
: Natural number–> whole and positive.
Find the natural numbers within the following set
Solution:
According to its definition, a natural number is a whole and positive number.
Therefore:
Natural number – whole and positive.
Number that is not natural - it is negative (does not meet the condition of being positive)
Number that is not natural - negative and also not whole
Number that is not natural - Not whole
Find the natural numbers within the following set
Solution:
Number that is not natural - Although it is positive, it is not an integer.
Number that is not natural - It is negative (does not meet the condition of being positive)
Natural number – Positive and also an integer
Number that is not natural - Although it is positive, it is not an integer.
Now that we already know how to identify natural numbers, we will move on to the exercises.
Find what is in the square
Solution:
In this exercise, there are only natural numbers, we need to find out which one would fit in the place of the square.
First, let's find out what the result of the parentheses is and rewrite the exercise.
We will obtain:
Now we can say that times something equals .
If we subtract from both sides we will get:
Now let's think, what number multiplied by five will give us .
We could also simply divide both sides by and obtain:
Another exercise with natural numbers
The general price of a pair of pants and four shirts is $.
The price of a pair of pants is equivalent to the price of shirts.
- What is the price of a pair of pants?
- What is the price of a shirt?
Solution:
First, let's organize the data.
We know that the price of a pair of pants is equal to the price of 2 shirts.
If we name the price of a shirt we can say that the price of a pair of pants is .
We also know that a pair of pants and shirts cost $ .
Let's write it as an exercise and we will get:
Let's solve the equation and it will give us:
Observe –> represents the price of shirt.
is the price of a pair of pants .
If then the answer will be:
The price of a pair of pants is $.
The price of a shirt is $.








