Find the Line Equation Through Points (5,0) and (1/2,4.5): Coordinate Method

Q: How do I handle the mixed number 4½ in calculations?

Convert 4½ to 4.5 (as a decimal) or 9/2 (as an improper fraction). Both work perfectly for slope calculations - just stay consistent with your choice!

Q: Why is the answer y + x = 5 instead of y = -x + 5?

Both forms are correct! y = -x + 5 is slope-intercept form, while y + x = 5 is standard form. You can rearrange: y = -x + 5 → y + x = 5 by adding x to both sides.

Q: What if I get the slope as a fraction instead of -1?

Check your arithmetic! With points (5,0) and (0.5, 4.5): $ \frac{0-4.5}{5-0.5} = \frac{-4.5}{4.5} = -1 $. The numbers divide evenly to give exactly -1.

Q: How do I know which point to use for finding b?

You can use either point! Both (5,0) and (0.5, 4.5) will give you b = 5 when you substitute into y = mx + b with m = -1.

Q: Can I check my answer using both points?

Absolutely! For y + x = 5: Point (5,0) gives 0 + 5 = 5 ✓, and point (0.5, 4.5) gives 4.5 + 0.5 = 5 ✓. Both should work!

Slope-Intercept Form with Mixed Number Coordinates

Find the equation of the line passing through the two points $(5,0),(\frac{1}{2},4\frac{1}{2})$

❤️ Continue Your Math Journey!

We have hundreds of course questions with personalized recommendations + Account 100% premium

Step-by-step video solution

Watch the teacher solve the problem with clear explanations

00:08 Let's find the algebraic representation of the function, shall we?

00:12 First, we're going to use a formula to determine the slope using two points. Ready?

00:18 At each point, remember, the left number is the X-axis and the right is the Y-axis. Easy, right?

00:26 Now, let's substitute these points into the formula with the data given, and find the slope. Let's do it!

00:42 Great! This number is the line's slope.

00:49 Next, we're going to use the line equation.

00:53 Substitute the point in the equation, following the data provided. You've got this!

00:59 Now, substitute the slope and solve for the intersection point, which we'll call 'B'. Keep going!

01:06 Let's isolate the intersection point, 'B'. Almost there!

01:12 And here is the intersection point with the Y-axis. Awesome job!

01:17 Now, plug this intersection point and the slope back into the line equation. You're doing amazing!

01:32 Let's tidy up the equation. Final steps!

01:39 And there you have it! That's the solution to our question. Well done!

Step-by-step written solution

Follow each step carefully to understand the complete solution

Understand the problem

Find the equation of the line passing through the two points $(5,0),(\frac{1}{2},4\frac{1}{2})$

Step-by-step solution

First, we will use the formula to find the slope of the straight line:

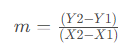
We replace the data and solve:

$\frac{(0-4.5)}{(5-0.5)}=\frac{-4.5}{4.5}=-1$

Now, we know that the slope is $-1$

We replace one of the points in the formula of the line equation:

$y=mx+b$

$(5,0)$

$0=-1\times5+b$

$0=-5+b$

$b=5$

Now we have the data to complete the equation:

$y=-1\times x+5$

$y=-x+5$

Final Answer

$y+x=5$

Key Points to Remember

Essential concepts to master this topic

Slope Formula: Use m = (y₂ - y₁)/(x₂ - x₁) with careful fraction conversion
Technique: Convert 4½ to 4.5, then calculate: (0-4.5)/(5-0.5) = -4.5/4.5 = -1
Check: Substitute both points into final equation y = -x + 5 ✓

Common Mistakes

Avoid these frequent errors

Converting mixed numbers incorrectly
Don't write 4½ as 4.2 or forget to convert it = wrong slope calculation! Mixed numbers must be converted properly: 4½ = 4.5 = 9/2. Always convert mixed numbers to decimals or improper fractions before calculating slope.

Practice Quiz

Test your knowledge with interactive questions

Look at the function shown in the figure.

When is the function positive?

FAQ

Everything you need to know about this question

How do I handle the mixed number 4½ in calculations?

Convert 4½ to 4.5 (as a decimal) or 9/2 (as an improper fraction). Both work perfectly for slope calculations - just stay consistent with your choice!

Why is the answer y + x = 5 instead of y = -x + 5?

Both forms are correct! y = -x + 5 is slope-intercept form, while y + x = 5 is standard form. You can rearrange: y = -x + 5 → y + x = 5 by adding x to both sides.

What if I get the slope as a fraction instead of -1?

Check your arithmetic! With points (5,0) and (0.5, 4.5): $\frac{0-4.5}{5-0.5} = \frac{-4.5}{4.5} = -1$ . The numbers divide evenly to give exactly -1.

How do I know which point to use for finding b?

You can use either point! Both (5,0) and (0.5, 4.5) will give you b = 5 when you substitute into y = mx + b with m = -1.

Can I check my answer using both points?

Absolutely! For y + x = 5: Point (5,0) gives 0 + 5 = 5 ✓, and point (0.5, 4.5) gives 4.5 + 0.5 = 5 ✓. Both should work!

🌟 Unlock Your Math Potential

Get unlimited access to all 18 Linear Functions questions, detailed video solutions, and personalized progress tracking.

📹

Unlimited Video Solutions

Step-by-step explanations for every problem

📊

Progress Analytics

Track your mastery across all topics

🚫

Ad-Free Learning

Focus on math without distractions

No credit card required • Cancel anytime