Consecutive numbers

What is a consecutive number?
A consecutive number is a number that is greater than the existing number by 1!
In other words, it's the number that comes right after the existing number.
For example -
The consecutive number of $3$ is $4$.
$4$ comes right after $3$.
We can add $3+1$
and obtain $4$.
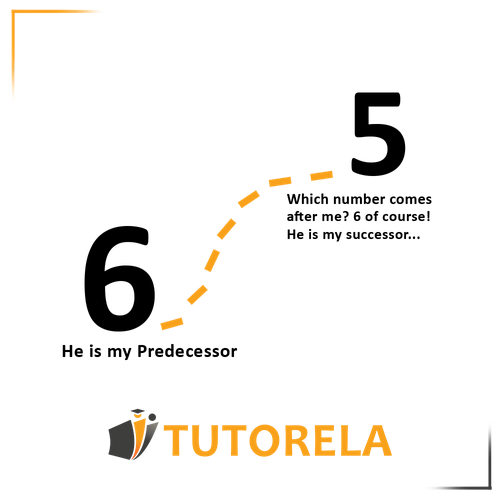
How will we remember what a consecutive number is?
Imagine any number - for example $5$

What is my consecutive number?
$6$ Of course! I follow it...

When you are asked -
What is the consecutive number after $5$,
ask yourself.. what number follows 5? 6 of course!
Or simply add $1$.

And now let's practice!
What is the consecutive number after $200$?
Answer –
$200+1=201$
201 is the answer.

Another exercise –
What is the consecutive number of $478$?
Answer:
$478+1=479$
$479$ is the answer.

Another exercise –
What is the consecutive number of $0$?

Solution -
$0+1=1$
$1$ is the answer.

What is the consecutive number after $79892$?
$79892+1=79893$
$79893$ is the answer.

Pay attention - until now we asked what is the consecutive number of-
What would happen if we asked:
$56$ is the consecutive number of ___
In this type of question, we would need to subtract $1$!
Essentially - the consecutive number is the number after adding.

Let's practice!
$70$ is the consecutive number of ?

Solution –
$70-1=69$
$​​​​​​​69$ is the solution.

Another exercise -
$786$ is the consecutive number of ?
$786-1=785$
$785$ is the answer.

Another exercise -
$86544$ is the consecutive number of?

Solution –
$86544-1=86543$
$86543$ is the solution.

Now to make it harder - let's mix between the 2 options:

What is the consecutive number after $79$?

Solution -
Let's find the consecutive number by adding $1$:
$79+1=80$
$80$ is the solution.

Another exercise –
$66$ is the consecutive number of?
$66$ is already the consecutive number so we subtract $1$:
$66-1=65$
$65$ is the answer!

Great! Now let's move on to consecutive number sequences!

If you were asked to write consecutive numbers from smallest to largest - for example $4$ consecutive numbers from smallest to largest,
you would need to write $4$ numbers that follow each other in sequence.
For example:
$21,22,23,24$
or for example:
$56,57,58,59$
or
$1,2,3,4$

$4$ consecutive numbers.

Question –
Are these $4$ consecutive numbers from smallest to largest?
$11,13,12,14$

The answer is no! The numbers need to be arranged in the correct sequence from smallest to largest to be called $4$ consecutive numbers.
If we were to arrange them like this:
$11,12,13,14$
The answer would be correct.

And what if we were asked whether these numbers are $4$ consecutive numbers from smallest to largest?
$70,71,73,72$

Answer -
The numbers do not meet the condition of $4$ consecutive numbers and only if they were arranged from smallest to largest in order like this -
$70,71,72,73$
Could they be considered to be consecutive numbers.
Let's move on to the sum of consecutive numbers!

Reminder-
The sum of numbers means we need to add the numbers together in order to obtain their sum.
Thanks to the commutative property, we can determine the order of addition and it shouldn't affect the result!

For example –
What is the sum of the numbers:
$2+14+8=$
If we calculate in order – First
$2+14=16$
Next
$16+8=24$
The answer will be $24$.
Even if we switch between the numbers and calculate like this:
$2+8=10$
$​​​​​​​10+14=24$
The answer will still be $24$.

Let's practice!
Write $4$ consecutive numbers from smallest to largest and calculate their sum –

Solution –
Here are four consecutive numbers as seen in the example:
$12,13,14,15$
Now let's calculate their sum :
$12+13=25$
$25+15=40$
$40+14=54$
$54$ is the sum of the consecutive numbers that we chose.