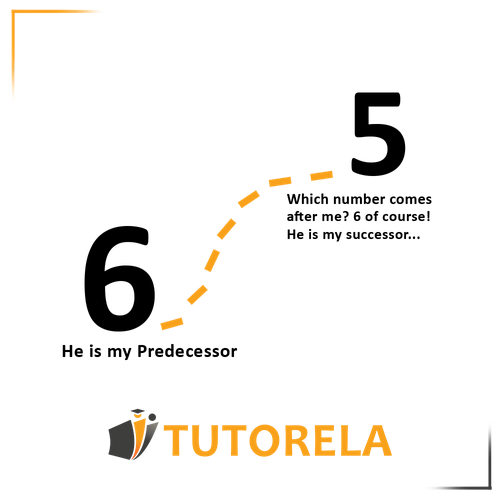
A consecutive number is a number that is greater by 1 than the existing number.
When we are asked -
The consecutive number of "any number" is...
We calculate as follows:
Consecutive Numbers Practice: Problems & Solutions Up to 100
Master consecutive numbers with step-by-step practice problems. Learn to find consecutive numbers, sequences, and sums with interactive exercises up to 100.
📚Master Consecutive Numbers with Interactive Practice
- Find the consecutive number after any given number by adding 1
- Identify which number comes before a consecutive number by subtracting 1
- Create sequences of 3, 4, or 5 consecutive numbers in ascending order
- Calculate the sum of consecutive number sequences using efficient methods
- Solve mixed problems combining consecutive number rules and operations
- Apply consecutive number concepts to real-world counting scenarios
Understanding Consecutive Numbers up to 100
Complete explanation with examples
Consecutive numbers
When we are asked -
"Some number" is the consecutive number of...
We calculate as follows:
Consecutive numbers sequence
Consecutive numbers from smallest to largest are numbers that follow one another in ascending order,
For example:
Sum of Consecutive Numbers
The sum of consecutive numbers is the addition of all consecutive numbers we have.
For example -
We can use the commutative and associative properties and calculate as seen below:
Practice Consecutive Numbers up to 100
Test your knowledge with 35 quizzes
Which number follows 81,900?
Examples with solutions for Consecutive Numbers up to 100
Step-by-step solutions included
Exercise #1
Which number succeeds the number 9209?
Step-by-Step Solution
To solve this problem, we'll proceed as follows:
- Identify the number we are working with, which is 9209.
- Apply the concept of finding a successor by adding 1 to this number.
- Perform the arithmetic calculation to find the next number.
Now, let's work through these steps:
Step 1: We are given the number 9209.
Step 2: To find its successor, we add 1: .
Step 3: Calculating this, we have .
Therefore, the successor of 9209 is .
Answer:
Exercise #2
Select the successor of the number 5449:
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given information
- Step 2: Apply the formula for finding a successor
- Step 3: Perform the addition calculation
Now, let's work through each step:
Step 1: The problem gives us the number 5449.
Step 2: To find the successor, we use the formula .
Step 3: Add 1 to 5449 to find its successor:
Therefore, the solution to the problem is .
Answer:
Exercise #3
Select the successor of the number 6599:
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given information.
- Step 2: Apply the appropriate formula for finding the successor.
- Step 3: Perform the calculation to find the successor.
Now, let's work through each step:
Step 1: The given number is 6599.
Step 2: We'll use the formula for the successor, which is to add 1 to the given number.
Step 3: Calculating the successor, we add 1 to 6599:
Therefore, the successor of 6599 is .
Answer:
Exercise #4
Select the predecessor of the number 2100:
Step-by-Step Solution
To solve this problem, we'll find the predecessor of 2100 by performing a simple calculation.
Let's outline the steps:
- Step 1: Identify the given number: .
- Step 2: Apply the formula for a predecessor: subtract 1 from the given number.
Now, let's perform the calculation:
Therefore, the predecessor of 2100 is .
Answer:
Exercise #5
Select the predecessor of the number 3140:
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given information
- Step 2: Apply the appropriate formula
- Step 3: Perform the necessary calculations
Now, let's work through each step:
Step 1: The problem gives us the number .
Step 2: To find the predecessor, we use the formula .
Step 3: Subtracting 1 from , we have .
Therefore, the predecessor of is .
Answer:
Frequently Asked Questions
What is a consecutive number in math?
+A consecutive number is a number that is exactly 1 greater than the existing number. For example, 6 is the consecutive number of 5 because 5 + 1 = 6. Consecutive numbers follow each other in counting order without any gaps.
How do you find consecutive numbers step by step?
+To find the consecutive number after any number, simply add 1. To find what number comes before a consecutive number, subtract 1. For example: consecutive number of 23 is 23 + 1 = 24, and 50 is the consecutive number of 50 - 1 = 49.
What are 4 consecutive numbers examples?
+Here are examples of 4 consecutive numbers: 1) 12, 13, 14, 15 2) 56, 57, 58, 59 3) 21, 22, 23, 24. These numbers must be arranged from smallest to largest with each number being exactly 1 more than the previous number.
How do you add consecutive numbers quickly?
+Use the commutative and associative properties to pair numbers efficiently. For example, with 23, 24, 25, 26: pair the outer numbers (23 + 26 = 49) and inner numbers (24 + 25 = 49), then add the pairs (49 + 49 = 98).
Can 0 have a consecutive number?
+Yes, the consecutive number of 0 is 1, because 0 + 1 = 1. Every whole number, including 0, has a consecutive number that follows it in the counting sequence.
What's the difference between consecutive and sequential numbers?
+Consecutive numbers are sequential numbers that differ by exactly 1 (like 5, 6, 7). Sequential numbers follow a pattern but may have different intervals (like 2, 4, 6, 8 which are sequential but not consecutive).
How do you solve consecutive number word problems?
+1) Identify if you need to find the next number (add 1) or previous number (subtract 1) 2) Check if numbers need to be in ascending order 3) For sums, add all consecutive numbers together 4) Use pairing methods for faster calculation when possible.
Are consecutive numbers always positive?
+No, consecutive numbers can be negative too. For example, -3, -2, -1, 0 are consecutive numbers. The rule of adding 1 to get the next consecutive number applies to all integers, both positive and negative.