In this article, you will learn everything you need to know about the special shape ellipse and also how to calculate its area.
Shall we begin?
Ellipse
Ellipse
This is our ellipse:
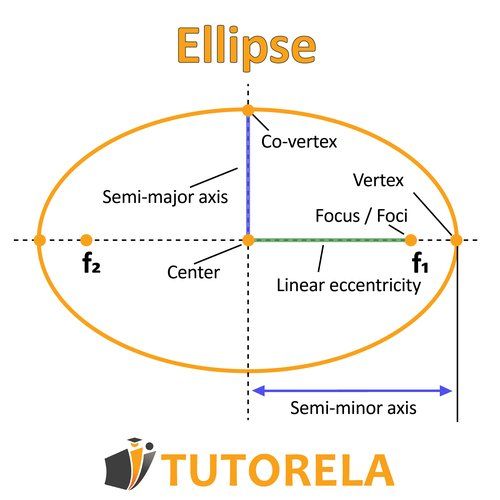
On the ellipse, we will draw the axes and in order to better understand the material.
The typical equation of the ellipse (with its center at ) is:
The intersection points of the ellipse with the axis are:
and –
The points of intersection of the ellipse with the axis are:
and
The foci of the ellipse are:
and
Important to know:
According to the definition of an ellipse, if we take any point on the circumference of the ellipse and draw one chord to one focus and another chord to the other focus,
we will find that their sum is equal to
How do we find ?
According to the formula
Ellipse
And now? For the real practice!
Here is the following ellipse equation:
Find and
Solution:
If we look at the ellipse equation, we see that in the denominator and are squared.
Therefore, we need to take the square root of and the square root of to identify and .
We get that:
Another exercise:
In front of you is an ellipse whose intersection points with the axis are
and its intersection points with the axis are and
Find the equation of the ellipse
Solution:
We know that –
The intersection points of the ellipse with the axis are:
and –
The intersection points of the ellipse with the axis are:
and
Therefore, if we substitute the given intersection points, we can immediately identify and .
Now we substitute the and of the ellipse into the ellipse equation:
And we get that the equation of the given ellipse is:
How do you calculate the area of an ellipse?
To calculate the area of an ellipse, you should be familiar with two more concepts.
In an ellipse, there is a major radius – the vertical one
and a minor radius – the horizontal one
Let's see this in the illustration:
*Illustration in a Word file*
- The major radius is on the axis and is marked in purple
- The minor radius is on the axis and is marked in pink
We will use the formula to calculate the area of an ellipse:
Area of an ellipse =
Note –
If you find the intersection points of the ellipse with the axis and the axis, you can find and which represent the distance of the ellipse from the axes and thus find the area of the ellipse.
And now to practice!
Here is the following ellipse equation:
Find \(a \) and \(b \).
Find the points of intersection with the \(X\) axis and the points of intersection with the \(Y\) axis.
Find the area of the ellipse.
Solution:
If we look at the ellipse equation, we see that in the denominator and
are squared.
Therefore, we need to take the square root of and the square root of to identify and
We get that:
It is known that:
The intersection points of the ellipse with the axis are:
and
The intersection points of the ellipse with the axis are:
and
Therefore, we simply substitute the and we found and get that:
The intersection points of the ellipse with the axis are:
and
The intersection points of the ellipse with the axis are:
and
To find the area of the ellipse, we need to find and
In fact, we already found them when we found the intersection points:
the distance from the center of the ellipse to the intersection with the axis
the distance from the center of the ellipse to the intersection with the axis
Substitute into the formula and get:
The area of the ellipse is cm²
Want to know more about the area of an ellipse? Click here








