There are various types of fractions that need to be known:
Types of Fractions
Types of Fractions
Simple Fraction
A simple fraction is the classic among all fractions and contains only a numerator and a denominator.
- The fraction line - symbolizes the division operation.
The numerator – represents the part of the whole (the relevant part we are asked about in the question – the thing that needs to be divided equally among everyone).
The denominator – represents the whole – the total – the total number of "pieces" there are.
Improper Fraction
An improper fraction is any number written like a fraction with a numerator and a denominator, but it is actually a whole number or a whole number with a fraction.
Mixed Fraction
A mixed number is a fraction composed of a whole number and a fraction, hence its name – it combines both whole numbers and fractions.
Decimal Fraction
A decimal fraction represents a non-whole number using a decimal point.
The decimal fraction can be without whole numbers at all or with whole number

Test yourself on simple fractions!
Without calculating, determine whether the quotient in the division exercise is less than 1 or not:
\( 5:6= \)
Types of Fractions
What is a fraction?
A fraction is essentially a part of the whole where the numerator is the part
and the denominator is the total whole.
For example - pizza will describe one pizza slice out of pizza slices that exist in a family-sized pizza.
Another example:
If there are balls in a bag and only of them are pink, we can say that the pink balls constitute of the balls in the bag.
Fractions can be represented in several forms:
Simple fraction
A simple fraction is the classic among all fractions and contains only a numerator and a denominator.
What does a simple fraction contain?
The fraction line - symbolizes the division operation.
The numerator – represents the part of the whole (the relevant part we are asked about in the question – the thing that needs to be divided equally among everyone).
The denominator – represents the whole – the total – the total number of "pieces" there are.
For example:
Dana had a birthday cake. Dana's mom cut the cake into equal slices.
At the birthday party, the children ate slices of cake in total, including Dana.
Present a simple fraction that represents the part of the cake that remains.
Solution:
The part of the cake that was eaten is slices out of , which means there are slices left out of , which is: .
If we simplify, we get .
Click here to learn more about a simple fraction
Without calculating, determine whether the quotient in the division exercise is less than 1 or not:
\( 1:2= \)
Match the following description with the corresponding fraction:
10 tickets are distributed equally among 9 couples.
Choose the fraction that corresponds to the following description:
11 shirts are shared equally between 8 players.
Improper fraction
An improper fraction is any number written like a fraction with a numerator and a denominator, but it is actually a whole number or a whole number with a fraction.
How can you remember this?
The word "improper" indicates that the fraction we see is not really a simple fraction but an improper one – "similar" to a simple fraction but actually it is not because it is whole or more than whole and not just a part of a whole.
Exercise:
In the orange cake recipe, you need one and a half cups of flour.
Describe the amount of flour in the cake using an improper fraction.
Solution:
A cup and a half is actually . Now let's convert this mixed number to an improper fraction:
How do you convert a mixed number to an improper fraction?
We multiply the number of wholes by the denominator.
To the result we obtained, we add the numerator – the final result will be the new numerator.
In the denominator – we don't change anything.
We get:
Click here to learn more about improper fractions
Mixed fraction
A mixed number is a fraction composed of a whole number and a fraction, hence its name – it combines both whole numbers and fractions.
The whole number appears to the left of the fraction, followed immediately by the fraction.
Examples of mixed numbers:
Advanced Exercise:
Romi asked her mom how much longer until their vacation in Spain.
Her mom replied: exactly two weeks and three days.
Represent the time until the vacation as a mixed number.
Solution:
Note, we need to express two weeks and three days using a mixed number.
Therefore, we express the two weeks as as a whole number and the three days as , meaning three days out of a week.
(The whole number in this case represents full weeks)
We get that: is the duration in a mixed number until the vacation in Spain.
Click here to learn more about mixed fractions
Match the following description with the corresponding fraction:
3 apples are distributed equally among two children.
Solve the following equation:
\( \frac{3}{4}-\frac{1}{6}=\text{ ?} \)
Without calculating, determine whether the quotient in the division exercise is less than 1 or not:
\( 5:6= \)
Decimal fraction
A decimal fraction represents a non-whole number using a decimal point.
The decimal fraction can be without whole numbers at all or with whole numbers.
The decimal point divides the fraction as follows:
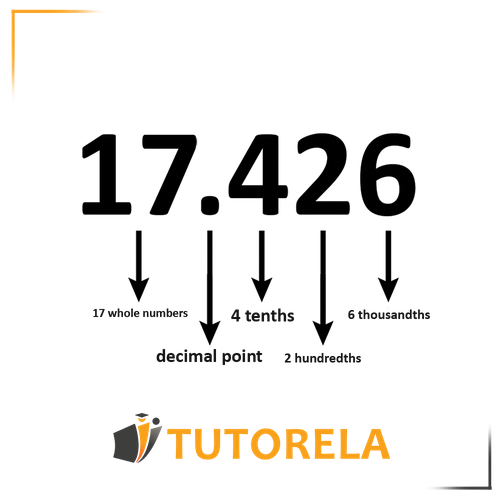
Another example:
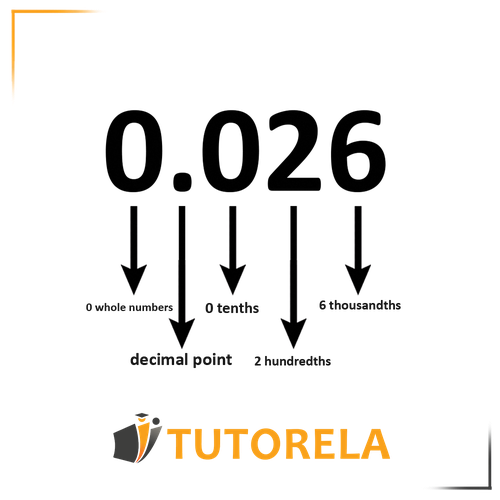
Comparison of decimal fractions
We will check the whole numbers – the decimal fraction with the larger whole number is the greater one.
If the whole numbers are the same, we will check the digits after the decimal point.
We will go digit by digit in order (starting from the tenths, hundredths, and so on).
If they are identical, we will continue.
If they are different, we will determine which fraction is greater accordingly.
Click here to learn more about decimal fractions
Without calculating, determine whether the quotient in the division exercise is less than 1 or not:
\( 1:2= \)
Match the following description with the corresponding fraction:
10 tickets are distributed equally among 9 couples.
Choose the fraction that corresponds to the following description:
11 shirts are shared equally between 8 players.
Examples with solutions for Simple Fractions
Exercise #1
Without calculating, determine whether the quotient in the division exercise is less than 1 or not:
Video Solution
Step-by-Step Solution
Note that the numerator is smaller than the denominator:
As a result, we can write it thusly:
Therefore, the quotient in the division exercise is indeed less than 1.
Answer
Less than 1
Exercise #2
Without calculating, determine whether the quotient in the division exercise is less than 1 or not:
Video Solution
Step-by-Step Solution
Note that the numerator is smaller than the denominator:
As a result, we can claim that:
Therefore, the fraction in the division problem is indeed less than 1.
Answer
Yes
Exercise #3
Match the following description with the corresponding fraction:
10 tickets are distributed equally among 9 couples.
Step-by-Step Solution
We need to understand that every fraction is actually a division exercise,
so when we divide 10 tickets among 9 people,
we are dividing 10 by 9
that is 10:9
The division exercise can also be written as a fraction

and that's the solution!
Answer
Exercise #4
Choose the fraction that corresponds to the following description:
11 shirts are shared equally between 8 players.
Step-by-Step Solution
To find the fraction that corresponds to the description of 11 shirts being shared equally among 8 players, we perform the following steps:
- Step 1: Identify the total number of shirts. Here, this number is 11.
- Step 2: Identify the total number of players. Here, this number is 8.
- Step 3: Set up the fraction where 11 is the number of shirts and 8 is the number of players.
This fraction represents how shirts are distributed among players, meaning each player receives of a shirt.
Therefore, the correct answer to the problem is , which corresponds to choice 3.
Answer
Exercise #5
Match the following description with the corresponding fraction:
3 apples are distributed equally among two children.
Step-by-Step Solution
Let's solve the problem step by step:
We are given 3 apples that need to be distributed equally among 2 children. This requires calculating how many apples each child receives, expressed as a fraction.
- Step 1: Identify how to divide the apples. We want each child to receive an equal share of the 3 apples. This implies a division problem: .
- Step 2: Set up the division as a fraction. When you divide 3 apples among 2 children equally, you are determining .
- Step 3: Express the result as a fraction. Each child receives apples.
Thus, when 3 apples are divided equally among 2 children, the result is represented by the fraction .
This matches with the correct choice provided, which is choice 4: .
Therefore, the solution to the problem is .
Answer
- Opposite numbers
- Elimination of Parentheses in Real Numbers
- Addition and Subtraction of Real Numbers
- Multiplication and Division of Real Numbers
- Integer powering
- Positive and negative numbers and zero
- Real line or Numerical line
- Sum of Fractions
- Subtraction of Fractions
- Multiplication of Fractions
- Division of Fractions
- Comparing Fractions
- Decimal Fractions
- What is a Decimal Number?
- Reducing and Expanding Decimal Numbers
- Addition and Subtraction of Decimal Numbers
- Comparison of Decimal Numbers
- Converting Decimals to Fractions
- Decimal fraction remainder
- Remainders









