When we are asked to round a number, we are actually asked to change it to the nearest whole and round number.
Rounding Numbers to 10,000 Practice Problems & Worksheets
Master rounding numbers to tens, hundreds, and thousands up to 10,000 with step-by-step practice problems, examples, and instant feedback for grades 3-5.
📚What You'll Practice
- Round 3-digit and 4-digit numbers to the nearest ten using the ones digit
- Round numbers to the nearest hundred by examining the tens digit
- Apply the rule: round up if digit is 5 or greater, down if less than 5
- Practice with numbers like 347, 283, and 2,849 to build confidence
- Use the tilde symbol (∼) to show rounded number relationships
- Distinguish between rounding to tens versus hundreds in multi-step problems
Understanding Rounding Numbers up to 10,000
Complete explanation with examples
Rounding Numbers
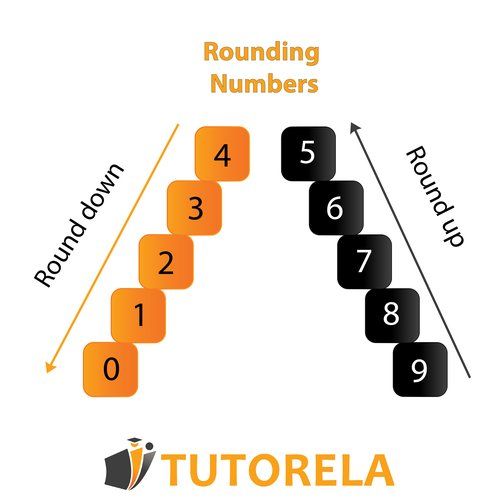
Rounding to tens
If the ones digit is or higher, we round up to the nearest tens, to the closest larger round number.
If the ones digit is less than , we round down to the nearest tens to the closest smaller round number.
Rounding to hundreds
If the tens digit is or higher, we round up to the nearest hundred.
If the tens digit is less than , we round down to the nearest hundred.
Practice Rounding Numbers up to 10,000
Test your knowledge with 6 quizzes
\( 431\approx\text{ ?} \)
Examples with solutions for Rounding Numbers up to 10,000
Step-by-step solutions included
Exercise #1
Choose the right answer:
Step-by-Step Solution
To solve the problem of finding the approximation of , follow these steps:
- Step 1: Determine which place value rounding is expected. Since smaller increments in hundreds and tens are presented in our choices, start with rounding to the nearest 10.
- Step 2: Look at the unit digit (3) in . Ensure proper positioning by analyzing what rounding to the nearest 10 will enact here.
- Step 3: Carry out: When rounding numbers, we determine if the parentheses value, , requests rounding up or down. When the units digit in this place value is below five, the rounding retains the lower outcome of these choices.
Looking at , examining its digits, the tens place is 3 and the units digit is 3, it is less than 5. Thus, the number rounds down to .
Therefore, rounding to the nearest 10 gives .
Answer:
Exercise #2
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the tens and units digits in 465.
- Step 2: Apply the rounding rule for the nearest ten.
- Step 3: Determine the rounded value based on the rule.
Now, let's work through each step:
Step 1: The number 465 has 6 in the tens place and 5 in the units place.
Step 2: To round to the nearest ten, we look at the units digit (5). According to rounding rules, if the digit is 5 or more, we round up.
Step 3: Since the units digit of 465 is 5, we round 460 up to 470.
Therefore, the rounded value of 465 to the nearest ten is .
Answer:
Exercise #3
Step-by-Step Solution
To round the number 1367 to the nearest hundred, we carry out the following steps:
- Step 1: Identify the digit in the tens place, which is '6' for 1367.
- Step 2: Apply the rounding rule where if the tens digit is 5 or greater, round up.
- Step 3: Since the tens digit is 6, we round up.
- Step 4: Replace the tens and units digits with zero.
- This results in rounding 1367 to 1400.
Thus, when rounding 1367 to the nearest hundred, we get .
Answer:
Exercise #4
Step-by-Step Solution
To solve this problem, we will round the number 52 to the nearest 10. Here's the step-by-step explanation:
- Step 1: Identify the ones digit of 52, which is 2.
- Step 2: Apply the rounding rule: if the ones digit is less than 5, round down; if it is 5 or more, round up.
- Step 3: Since the ones digit of 52 is 2, which is less than 5, we will round down to the nearest multiple of 10.
- Step 4: The nearest multiple of 10 below 52 is 50.
Therefore, when 52 is rounded to the nearest 10, it becomes .
Answer:
Exercise #5
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the tens and units digits of the number 68.
- Step 2: Use rounding rules to determine if we round up or down.
- Step 3: Replace the units digit appropriately to find the rounded number.
Now, let's work through each step:
Step 1: The tens digit of 68 is 6, and the units digit is 8.
Step 2: Since the units digit (8) is 5 or greater, we round up the number 68.
Step 3: After rounding up, we replace the units digit with 0, resulting in the rounded number 70.
Therefore, the solution to the problem is .
Answer:
Frequently Asked Questions
How do you round numbers to the nearest ten?
+Look at the ones digit. If it's 5 or greater, round up to the next ten. If it's less than 5, round down. For example, 23 rounds down to 20 (ones digit is 3), while 46 rounds up to 50 (ones digit is 6).
What's the difference between rounding to tens and hundreds?
+When rounding to tens, examine the ones digit. When rounding to hundreds, examine the tens digit. The number 347 rounds to 350 (nearest ten) but 300 (nearest hundred) because you look at different digits.
Why do we round 5 up instead of down?
+The rounding rule states that 5 and above rounds up, while 4 and below rounds down. This creates a balanced system where half the digits (0-4) round down and half (5-9) round up, making calculations fair and consistent.
How do you round 4-digit numbers like 2,847?
+Follow the same rules but pay attention to what place you're rounding to:
• To nearest ten: look at ones digit (7) → rounds to 2,850
• To nearest hundred: look at tens digit (4) → rounds to 2,800
• To nearest thousand: look at hundreds digit (8) → rounds to 3,000
What does the tilde symbol (∼) mean in rounding?
+The tilde symbol (∼) shows that a number has been rounded. For example, 23 ∼ 20 means "23 rounds to 20." It's mathematical notation that clearly indicates an approximation rather than an exact value.
When should students learn rounding numbers?
+Students typically learn rounding in grades 3-5. They start with rounding to tens, then progress to hundreds and thousands. Mastering rounding helps with estimation, mental math, and understanding place value concepts.
What are common mistakes when rounding numbers?
+Common errors include: looking at the wrong digit (checking ones instead of tens for hundreds), forgetting the "5 rounds up" rule, and rounding multiple times instead of going directly to the target place value. Practice identifying which digit to examine first.
How does rounding help in real life?
+Rounding helps estimate costs when shopping, approximate distances and time, simplify large numbers in reports, and make quick mental calculations. For example, rounding $23.47 to $20 helps estimate if you have enough money for a purchase.