Extended Distributive Property Practice Problems & Worksheets

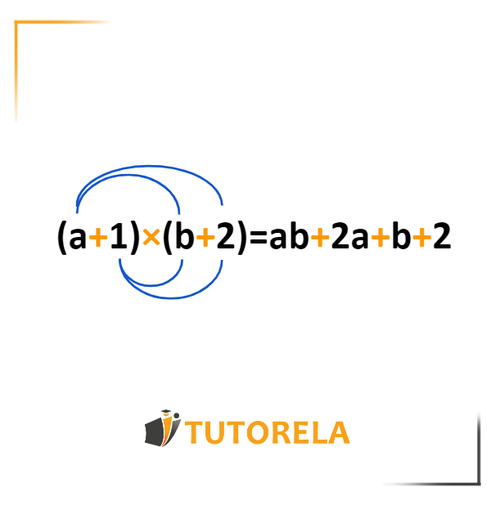
In order to simplify the given expression, open the parentheses using the extended distribution law:

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$

Note that in the formula template for the above distribution law, it is a given that the operation between the terms inside of the parentheses is addition. Furthermore the sign preceding the term is of great significance and must be taken into consideration;

Proceed to apply the above formula to the expression to open out the parentheses.

$(x-6)(x+8)\\ \downarrow\\ \big(\textcolor{red}{x}+\textcolor{blue}{(-6)}\big)(x+8)\\$Let's begin then with opening the parentheses:

$\big(\textcolor{red}{x}+\textcolor{blue}{(-6)}\big)(x+8)\\ \textcolor{red}{x}\cdot x+\textcolor{red}{x}\cdot8+\textcolor{blue}{(-6)}\cdot x+\textcolor{blue}{(-6)}\cdot8\\ x^2+8x-6x-48$

To calculate the above multiplications operations we used the multiplication table as well as the laws of exponents for multiplication between terms with identical bases:

$a^m\cdot a^n=a^{m+n}$

In the next step we'll combine like terms which we define as terms where the variable (or variables ), in this case x, have identical exponents . (Note that in the absence of one of the variables from the expression, we'll consider its exponent as zero power due to the fact that raising any number to the zero power yields the result 1) Apply the commutative property of addition and proceed to arrange the expression from highest to lowest power from left to right (Note: treat the free number as having zero power):
$\textcolor{purple}{x^2}\textcolor{green}{+8x-6x}\textcolor{orange}{-48}\\ \textcolor{purple}{x^2}\textcolor{green}{+2x}\textcolor{orange}{-48}\\$When combining like terms as shown above, we highlighted the different terms using colors, as well as treating the sign preceding the term as an inseparable part of it.

The correct answer is answer A.

In order to solve the given problem, we will use the FOIL method. FOIL stands for First, Outer, Inner, Last. This helps us to systematically expand the product of the two binomials:

• Step 1: Multiply the First terms.

The first terms of each binomial are $x$ and $x$. Multiply these together to obtain $x \times x = x^2$.

• Step 2: Multiply the Outer terms.

The outer terms are $x$ and $-4$. Multiply these. together to obtain $x \times -4 = -4x$.

• Step 3: Multiply the Inner terms.

The inner terms are $2$ and $x$. Multiply these together to obtain $2 \times x = 2x$.

• Step 4: Multiply the Last terms.

The last terms are $2$ and $-4$. Multiply these together to obtain $2 \times -4 = -8$.

Proceed to combine all these results together:

$x^2 - 4x + 2x - 8$

Finally, combine like terms:

Combine $-4x$ and $2x$ to obtain $-2x$.

The expanded form of the expression is therefore:

$x^2 - 2x - 8$

Thus, the solution to the problem is $x^2 - 2x - 8$, which corresponds to choice 1.

To solve this problem, we need to multiply the binomials $(x-6)$ and $(x+2)$ using the distributive property (FOIL method):

• First: Multiply the first terms: $x \cdot x = x^2$
• Outer: Multiply the outer terms: $x \cdot 2 = 2x$
• Inner: Multiply the inner terms: $-6 \cdot x = -6x$
• Last: Multiply the last terms: $-6 \cdot 2 = -12$

Now, we have the terms: $x^2$, $2x$, $-6x$, and $-12$.
We combine the linear terms:

$x^2 + 2x - 6x - 12 = x^2 - 4x - 12$

This is the expanded form of the quadratic expression in standard form.
Therefore, the solution to the problem is $x^2 - 4x - 12$.

To solve this problem, we'll follow these steps:

• Step 1: Identify the structure of the expression
• Step 2: Apply the difference of squares formula
• Step 3: Simplify the expression

Now, let's work through each step:
Step 1: The expression is $(x+y)(x-y)$, which resembles the difference of squares. Step 2: Using the formula for the difference of squares, $(a+b)(a-b) = a^2 - b^2$, we set $a = x$ and $b = y$. Step 3: Applying the formula, we have:

$(x+y)(x-y) = x^2 - y^2$.

Therefore, the solution to the problem is $x^2-y^2$.

Simplify this expression paying attention to the order of arithmetic operations. Exponentiation precedes multiplication whilst division precedes addition and subtraction. Parentheses precede all of the above.

Therefore, let's first start by simplifying the expressions within the parentheses. Then we can proceed to perform the multiplication between them:

$(3+20)\cdot(12+4)=\\ 23\cdot16=\\ 368$

Therefore, the correct answer is option A.