$$ \frac{35.3}{1,000,000m^3} $$

Units of Volume | Tutorela

Every three-dimensional body has volume. For example, a ball or pyramid are bodies with volume. The volume of a body is our way of measuring the space that said body occupies in space.

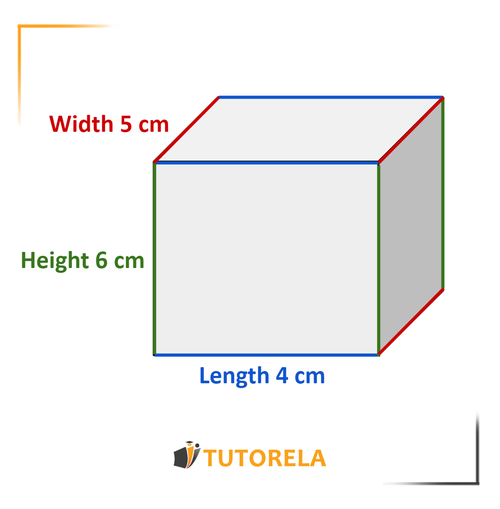
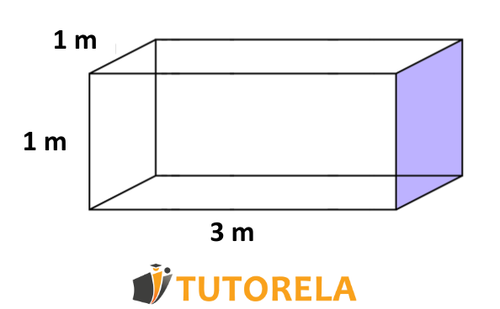
For example, let's observe a cube whose length of each of its sides is $1\operatorname{cm}$ , like this one:

a cube whose length of each of its sides is 1 cm

To calculate the volume of the cube we will use the known formula: $Length\times ~width\times~height$

In this case, the three dimensions are equal and, therefore, we will note:

$V=1\operatorname{cm}\times1\operatorname{cm}\times1\operatorname{cm}=1\operatorname{cm}^3$

V is the letter used to abbreviate the word volume in exercises and is used to designate volumes.

That is, we found that the volume of the cube is $1~cm³=$ cubic centimeter (cm raised to the third power)

Known volume measurement units:

$1~m³=1000~dm³=1,000,000~cm³$

$1~dm³=1000~cm³$

Additionally, there are measurements that we primarily use for measuring liquids:

$1~L=1~dm³=1,000~cm³$

$1~liter=1000~milliliters$

$1~milliliter = 1~cm³$

$1000~liters=1~m³$

Detailed explanation

Start practice

Test yourself on volume units!

How many cm³ are there in a m³?

Practice more now

The function of volume units is to quantify or measure the volume of objects. Since it is a three-dimensional unit, these units are always expressed in cubic powers.

For example, cubic centimeter $\operatorname{cm}^3$ and cubic meter $\left(m^3\right)$ . When referring to liquids, volume is usually measured in liters or gallons.

Let's analyze a simple exercise:

We have a box with the following measurements:

$Length~4~cm$

$Width~5~cm$

$Height~6~cm$

$4~\operatorname{cm}\times~5\operatorname{cm}\times~6\operatorname~{cm}=120$

$Length~4 ~cm\times ~width ~5 ~cm\times ~height ~6 ~cm$

if we need to calculate its volume.

In this case, the calculation is quite simple. We will calculate the volume of the box by multiplying the three measurements together. The result is $120~cm^3$ . It is crucial to highlight that, because we multiply cm by cm by cm three times, the result is given in $\operatorname{cm}^3$ , that is, cubic cm (cm raised to the third power).

If you are interested in this article, you may also be interested in the following articles:

On the Tutorela website you can find a variety of mathematics articles

Volume Measurements

Example 1

How many liters of water can the illustrated box hold?:

Let's remember that the formula to calculate the volume of a box is:

$Length\times width\times ~height$ .

Let's calculate the volume of the box:

$V=1~m\times1m\times3~m=3~m^3$

$1~m³=1000~dm³=1,000,000~cm³$

We found that the volume of the box is $3~m³$ (cubic meters).

Now we must convert the result to liters to answer the question.

Let's remember that $1~m³=1000$ liters.

Therefore:

$3~m³=3000$ liters.

That is, the amount of water that we can pour into the box is $3000$ liters.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Convert $$ 6.8dm^3 $$ into milliliters.

Question 2

How many milliliters are in a liter?

Question 3

What is 100 m³ written as cm³?

Example 2

How many liters are $10,000~cm³$ ?

Let's remember that:

$1,000~cm³=1 liter$

Therefore:

$10,000\operatorname{cm}³=10\times1000\operatorname{cm}³=10\times1~Liter=10~Liters$

That is, we found that $10,000~cm³$ are equivalent to $10$ liters.

Examples and exercises with solutions of volume units

Exercise #1

Convert $61\frac{1}{2}cm^3$ into cubic decimeter.

Video Solution

Step-by-Step Solution

Let's solve the problem through a series of steps for ease of understanding:

Step 1: Identify the volume in cubic centimeters.
The given volume is $61\frac{1}{2} \, \text{cm}^3$ .
Step 2: Convert the mixed number to an improper fraction.
The mixed number $61\frac{1}{2}$ can be rewritten as $61 + \frac{1}{2}$ which equals $\frac{122}{2} + \frac{1}{2} = \frac{123}{2}$ . This is equivalent to 61.5 cubic centimeters.
Step 3: Convert cubic centimeters to cubic decimeters.
Using the fact that $1 \, \text{dm}^3 = 1000 \, \text{cm}^3$ , we divide the given volume by 1000 to convert from cubic centimeters to cubic decimeters.
$\frac{123}{2} \div 1000 = \frac{123}{2000} = \frac{61.5}{1000}$

Therefore, the volume in cubic decimeters is $\frac{61.5}{1000} \, \text{dm}^3$ .

Upon examining the available choices, choice 1: $\frac{61.5}{1000 \, \text{dm}^3}$ is the correct answer.

The solution to the problem is $\frac{61.5}{1000 \, \text{dm}^3}$ .

Answer

$\frac{61.5}{1000dm^3}$

Exercise #2

What is 100 m³ written as cm³?

Video Solution

Step-by-Step Solution

To convert 100 m³ to cm³, follow these steps:

Step 1: Understand the relationship between meters and centimeters. We know that 1 meter equals 100 centimeters.
Step 2: Determine the volume in cubic centimeters for 1 cubic meter. Since 1 m = 100 cm, we have $1 \text{ m}^3 = (100 \, \text{cm})^3$ .
Step 3: Calculate $(100 \, \text{cm})^3$ . This results in $100 \times 100 \times 100 = 1,000,000$ cm³.
Step 4: Since we need to convert 100 m³, multiply the result for 1 m³ by 100. Thus, $100 \text{ m}^3 = 100 \times 1,000,000 \, \text{cm}^3 = 100,000,000 \, \text{cm}^3$ .

Therefore, 100 m³ is equivalent to $100,000,000 \, \text{cm}^3$ .

From the given choices, the correct choice is choice 3, which is $100,000,000 \, \text{cm}^3$ .

Answer

$100,000,000cm^3$

Exercise #3

What is 18 liters written in milliliters?

Video Solution

Step-by-Step Solution

To convert 18 liters to milliliters, we will follow these steps:

Identify the conversion factor from liters to milliliters.
Multiply the given number of liters by this conversion factor.

Step 1: The conversion factor is $1 \text{ liter} = 1000 \text{ milliliters}$ .

Step 2: Multiply 18 liters by 1000 to convert it to milliliters:

$18 \times 1000 = 18000$ milliliters.

Thus, 18 liters is equal to $18,000$ milliliters.

Therefore, the correct answer is $\text{choice 3}: 18,000 \text{ ml}$ . The answer, when compared to the choices, confirms that choice 3 is indeed the correct one.

Answer

$18,000ml$

Exercise #4

Convert $6.8dm^3$ into milliliters.

Video Solution

Step-by-Step Solution

To convert $6.8dm^3$ into milliliters, we'll follow these steps:

Step 1: Identify the given volume in cubic decimeters, which is $6.8dm^3$ .
Step 2: Use the conversion factor that $1dm^3 = 1000ml$ .
Step 3: Multiply the given volume by the conversion factor to convert cubic decimeters to milliliters.

Now, let's perform the conversion:
Given: $6.8dm^3$

Using the conversion factor, we calculate:
$6.8dm^3 \times 1000ml/dm^3 = 6800ml$

Therefore, the volume of $6.8dm^3$ is equivalent to $6800ml$ .

Answer

$6800ml$

Exercise #5

143535 milliliters are? liters

Video Solution

Step-by-Step Solution

To solve the problem of converting 143535 milliliters to liters, follow these steps:

The given quantity is 143535 milliliters (ml).
Use the conversion factor: $1 \text{ liter} = 1000 \text{ milliliters}$ .
Convert milliliters to liters by dividing the milliliters by 1000.

Let's perform the calculation:
$143535 \text{ ml} \div 1000 = 143.535 \text{ liters}$

This calculation shows that 143535 milliliters equals 143.535 liters.

Therefore, the solution to the problem is $143.535l$ .

Answer

$143.535l$

Review Questions

What are the units of volume?

As we have seen, everything that needs to be measured has its specific unit of measure. In the case of volume units, being a three-dimensional measure, that is, an object that has length, width, and height, its volume can be calculated. Therefore, we can measure it either in liters or milliliters, but if the objects have units of length, then the most common units in volume can be: $\operatorname{cm}^3$ , $\operatorname{m}^3$ , $\operatorname{dam}^3$ , $\operatorname{hm}^3$ , $\operatorname{dm}^3$ , $\operatorname{mm}^3$ , although it can also be measured in gallons and other volume units.

How are volume units written?

Being a unit of measure and as we said it is a three-dimensional unit, the measures are expressed to the third power, that is, as we have three dimensions length, width, and height, then suppose that its units are in $\operatorname{cm}$ , then to calculate the volume it will be:

$\operatorname{cm}\times cm\times cm=cm^3$

If its lengths are $\operatorname{m}$ , then the volume will be written in $\operatorname{m}^3$

What is the dimension of volume?

Being a dimension that is derived from length and by multiplying length, width, and height we will obtain a dimension to the cube. Or by making a conversion of volume units, that is, cubic, we can obtain an equivalence to liters, milliliters, or gallons.

Do you know what the answer is?

Question 1

143535 milliliters are? liters

Question 2

Convert $$ 16,848dm^3 $$ into liters.

Question 3

Convert $$ 1.6l $$ into milliliters.

Start practice

Units of Volume

Test yourself on volume units!

Volume Measurements

Example 1

Example 2

Examples and exercises with solutions of volume units

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

Review Questions

More Questions

Volume Units