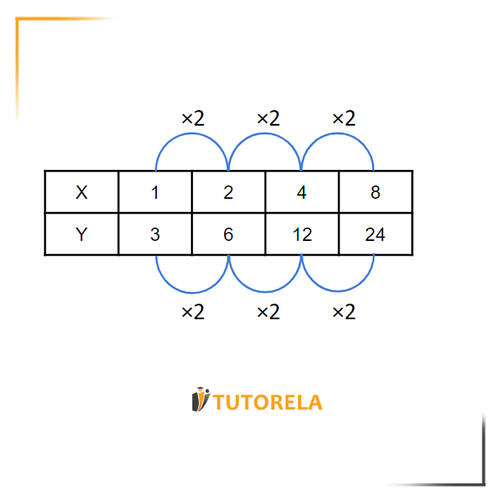
Direct Proportion - Examples, Exercises and Solutions

What is direct proportion?

Direct proportionality indicates a situation in which, when one term is multiplied by a certain amount, the same exact thing happens to the second term.

In the same way, when one term is divided by a certain amount, the same exact thing happens to the second term.

The ratio between both magnitudes remains constant.

Let's observe an example that illustrates this concept.

Practice Direct Proportion

Question 1

Given the rectangle ABCD

AB=X the ratio between AB and BC is equal to $\sqrt{\frac{x}{2}}$

We mark the length of the diagonal $$ A $$ with $$ m $$

Check the correct argument:

Question 2

Given the rectangle ABCD

AB=X

The ratio between AB and BC is $\sqrt{\frac{x}{2}}$

We mark the length of the diagonal A the rectangle in m

Check the correct argument:

Question 3

There are two circles.

The length of the diameter of circle 1 is 4 cm.

The length of the diameter of circle 2 is 10 cm.

How many times larger is the area of circle 2 than the area of circle 1?

Question 4

There are two circles.

The length of the radius of circle 1 is 6 cm.

The length of the diameter of circle 2 is 12 cm.

How many times greater is the area of circle 2 than the area of circle 1?

Question 5

There are two circles.

One circle has a radius of 4 cm, while the other circle has a radius of 10 cm.

How many times greater is the area of the second circle than the area of the first circle?

Examples with solutions for Direct Proportion

Exercise #1

Given the rectangle ABCD

AB=X the ratio between AB and BC is equal to $\sqrt{\frac{x}{2}}$

We mark the length of the diagonal $A$ with $m$

Check the correct argument:

Video Solution

Step-by-Step Solution

Let's find side BC

Based on what we're given:

$\frac{AB}{BC}=\frac{x}{BC}=\sqrt{\frac{x}{2}}$

$\frac{x}{BC}=\frac{\sqrt{x}}{\sqrt{2}}$

$\sqrt{2}x=\sqrt{x}BC$

Let's divide by square root x:

$\frac{\sqrt{2}\times x}{\sqrt{x}}=BC$

$\frac{\sqrt{2}\times\sqrt{x}\times\sqrt{x}}{\sqrt{x}}=BC$

Let's reduce the numerator and denominator by square root x:

$\sqrt{2}\sqrt{x}=BC$

We'll use the Pythagorean theorem to calculate the area of triangle ABC:

$AB^2+BC^2=AC^2$

Let's substitute what we're given:

$x^2+(\sqrt{2}\sqrt{x})^2=m^2$

$x^2+2x=m^2$

Answer

$x^2+2x=m^2$

Exercise #2

Given the rectangle ABCD

AB=X

The ratio between AB and BC is $\sqrt{\frac{x}{2}}$

We mark the length of the diagonal A the rectangle in m

Check the correct argument:

Video Solution

Step-by-Step Solution

Given that:

$\frac{AB}{BC}=\sqrt{\frac{x}{2}}$

Given that AB equals X

We will substitute accordingly in the formula:

$\frac{x}{BC}=\frac{\sqrt{x}}{\sqrt{2}}$

$x\sqrt{2}=BC\sqrt{x}$

$\frac{x\sqrt{2}}{\sqrt{x}}=BC$

$\frac{\sqrt{x}\times\sqrt{x}\times\sqrt{2}}{\sqrt{x}}=BC$

$\sqrt{x}\times\sqrt{2}=BC$

Now let's focus on triangle ABC and use the Pythagorean theorem:

$AB^2+BC^2=AC^2$

Let's substitute the known values:

$x^2+(\sqrt{x}\times\sqrt{2})^2=m^2$

$x^2+x\times2=m^2$

We'll add 1 to both sides:

$x^2+2x+1=m^2+1$

$(x+1)^2=m^2+1$

Answer

$m^2+1=(x+1)^2$

Exercise #3

There are two circles.

The length of the diameter of circle 1 is 4 cm.

The length of the diameter of circle 2 is 10 cm.

How many times larger is the area of circle 2 than the area of circle 1?

Video Solution

Answer

$6\frac{1}{4}$

Exercise #4

There are two circles.

The length of the radius of circle 1 is 6 cm.

The length of the diameter of circle 2 is 12 cm.

How many times greater is the area of circle 2 than the area of circle 1?

Video Solution

Answer

They are equal.

Exercise #5

There are two circles.

One circle has a radius of 4 cm, while the other circle has a radius of 10 cm.

How many times greater is the area of the second circle than the area of the first circle?

Video Solution

Answer

$6\frac{1}{4}$

Question 1

How many times longer is the radius of the red circle than the radius of the blue circle?

Question 2

How many times longer is the radius of the red circle, which has a diameter of 24, than the radius of the blue circle, which has a diameter of 12?

Question 3

How many times longer is the radius of the red circle than the radius of the blue circle?

Question 4

How many times longer is the radius of the red circle (14 cm) than the radius of the blue circle, which has a diameter of 7?

Question 5

How many times longer is the radius of the red circle than the radius of the blue circle?

Exercise #6

How many times longer is the radius of the red circle than the radius of the blue circle?

Video Solution

Answer

Exercise #7

How many times longer is the radius of the red circle, which has a diameter of 24, than the radius of the blue circle, which has a diameter of 12?

Video Solution

Answer

Exercise #8

How many times longer is the radius of the red circle than the radius of the blue circle?

Video Solution

Answer

$2$

Exercise #9

How many times longer is the radius of the red circle (14 cm) than the radius of the blue circle, which has a diameter of 7?

Video Solution

Answer

Exercise #10

How many times longer is the radius of the red circle than the radius of the blue circle?

Video Solution

Answer

$2\frac{1}{2}$

Question 1

There are 18 balls in a box, $\frac{2}{3}$ of which are white.

How many white balls are there in the box?

Question 2

In a box there are 28 balls, $\frac{1}{4}$ of which are orange.

How many orange balls are there in the box?

Question 3

ABCD is a deltoid with an area of 58 cm².

DB = 4

AE = 3

What is the ratio between the circles that have diameters formed by AE and and EC?

Exercise #11

There are 18 balls in a box, $\frac{2}{3}$ of which are white.

How many white balls are there in the box?

Video Solution

Answer

Exercise #12

In a box there are 28 balls, $\frac{1}{4}$ of which are orange.

How many orange balls are there in the box?

Video Solution

Answer

Exercise #13

ABCD is a deltoid with an area of 58 cm².

DB = 4

AE = 3

What is the ratio between the circles that have diameters formed by AE and and EC?

Video Solution

Answer

3:26

Topics learned in later sections