The midsegment of a trapezoid divides into two equal parts the two sides from which it extends and, in addition, is parallel to both bases of the trapezoid and measures half the length of these.
Let's see the properties of the midsegment of a trapezoid in the following illustration:
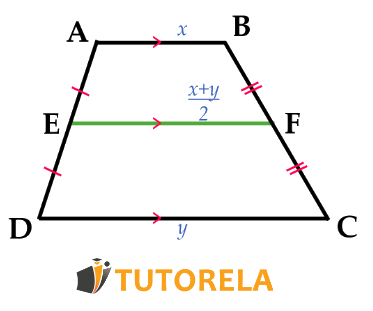
If Midsegment
then:
Given an isosceles trapezoid, is the dashed segment a middle segment of the trapezoid?
Is the dashed segment the midsegment of the isosceles trapezoid below?
In which figure is the dotted line the midsegment in the trapezoid?
In which figure is the dashed line the midsection of the trapezoid?
Below is an isosceles trapezium.
EF is parallel to the base of the trapezium.
True or false: EF is the midsection of the trapezoid.
Given an isosceles trapezoid, is the dashed segment a middle segment of the trapezoid?
Not true
Is the dashed segment the midsegment of the isosceles trapezoid below?
No
In which figure is the dotted line the midsegment in the trapezoid?
In which figure is the dashed line the midsection of the trapezoid?
Below is an isosceles trapezium.
EF is parallel to the base of the trapezium.
True or false: EF is the midsection of the trapezoid.
True
The quadrilateral ABCD is an isosceles trapezoid.
EF the midsegment.
Calculate the length of X.
The quadrilateral ABCD is a trapezoid.
EF is the midsegment.
Calculate EF.
The quadrilateral ABCD is a trapezoid.
EF is the midsection.
Calculate CD.
EF is the midsegment of the trapezoid ABCD.
Calculate the length of EF.
EF is the midsegment of the trapezoid ABCD.
Calculate the length of EF.
The quadrilateral ABCD is an isosceles trapezoid.
EF the midsegment.
Calculate the length of X.
11
The quadrilateral ABCD is a trapezoid.
EF is the midsegment.
Calculate EF.
6
The quadrilateral ABCD is a trapezoid.
EF is the midsection.
Calculate CD.
16
EF is the midsegment of the trapezoid ABCD.
Calculate the length of EF.
12
EF is the midsegment of the trapezoid ABCD.
Calculate the length of EF.
11
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
2
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
9
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
7
The quadrilateral ABCD is a trapezoid, EF is the middle section.
Find X
3