Reminder of the definition?
Where:
is the base of the log
is the exponent we raise the log base to in order to obtain the number inside the log.
is what appears inside the log, it can also appear in parentheses.
Multiplication of Logarithms
Multiplication of Logarithms
Reminder - Logarithms
Multiplication of logarithms with the same base
According to the rule
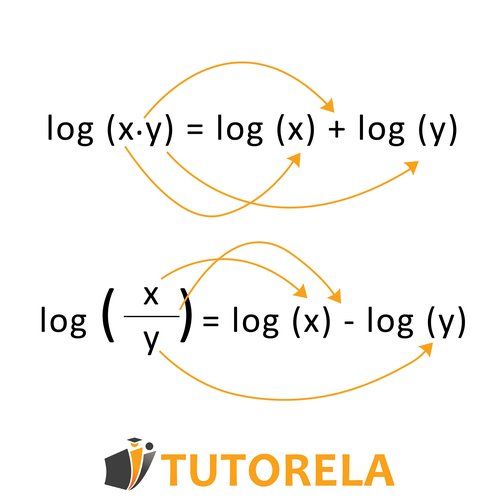
When the content of the log is a multiplication expression, we can split it into an addition expression – logs will have the same base.
The first log will be with the first term in the multiplication and the second log will be with the second term in the multiplication.
A multiplication exercise can be converted to an addition exercise and an addition exercise to a multiplication exercise with one log according to the rule as long as the base is the same.
Test yourself on multiplication of logarithms!
\( \log_49\times\log_{13}7= \)
Multiplication of Logarithms
Multiplication of logarithms with the same base
In order to solve perform the multiplication of logarithms, you need to know the following rule:
When there is multiplication inside the log, we can split the log into an addition problem with the same base where one log will have the content of one of the factors and the second log will have the content of the second factor.
You can convert the multiplication problem to an addition problem and an addition problem to a multiplication problem with one log according to the rule as long as the base is the same.
Let's look at an example:
We have an expression with a logarithm containing a multiplication operation. If we were to multiply what's inside of the parentheses, we would obtain something like this:
Of course, thanks to the rule, we can solve this exercise in a much easier and faster way.
We just need to split the exercise into an addition exercise with identical bases - in this exercise the base is .
It should look like this:
Now we can solve the exercise with greater ease!
Reminder -
The definition of a logarithm is:
Where:
is the base of the logarithm
is what appears inside the logarithm. It can also appear in parentheses.
is the exponent to which we raise the base of the logarithm to obtain the number inside the logarithm.
And so we ask ourselves - to what power do we need to raise to in order to obtain ? The answer is .
And to what power do we need to raise to in order to obtain ? The answer is .
We obtained the following:
Let's solve another exercise!
Solution:
To solve this exercise, we'll use the rule we learned about multiplying logarithms.
We can split the exercise into an addition exercise where the base is identical and equals .
As follows:
Now we can solve the problem more easily.
We know that in order to obtain we need to raise to the power of therefore
and in order to obtain we need to raise to the power of therefore
Let's substitute the data into the exercise as follows:
is the final answer.
Let's proceed to another exercise!
\(log_62+log_618=\
Pay attention! At first glance, this exercise appears to be an addition of logarithms with the same base... however! We are using the rule we learned about multiplying logarithms!
Solution Method:
Let's first try to solve the exercise without the rule -
If we think about which power we need to raise to in order to obtain ... we encounter a problem. This is not an intuitive solution
The again encounter the same problem for
Which power do we need to raise to in order to obtain ? Also a good question..
Therefore, we use the rule that states we can multiply the log contents with the same base. As seen below:
How wonderful! We now understand that in order to reach we need to raise to the power of !
Therefore the solution is . This is the final answer.
What did we learn? The multiplication rule we learned follows the commutative property.
It works on both sides - you can convert a multiplication expression into an addition expression, and an addition expression can be converted into a single log with multiplied content.
However - only if the base is identical.
Note - If there is multiplication of logarithms with different bases, you can try to convert the log base according to the rules you learned.
\( \log_mn\times\log_zr= \)
\( \log_54\times\log_23= \)
\( \log_37\times\log_79= \)
Examples with solutions for Multiplication of Logarithms
Exercise #1
Video Solution
Step-by-Step Solution
To solve the problem , we'll employ the change of base formula for logarithms:
- Step 1: Apply the change of base formula to each logarithm.
- Step 2: Use logarithm properties and analyze transformations for a match with choices.
Now, let's work through each step:
Step 1: Use the change of base formula on each log:
and , where and are arbitrary positive bases.
Both expressions use a common base not relevant for the solution but illustrate the transformation ability.
Step 2: We'll recombine and look for products that can utilize these, such as:
becomes
Applying cross multiplication or iteration forms, the structure aligns with the multiplication identity for this problem due to independence of base.
Therefore, the transformed expression satisfying the criteria is .
Answer
Exercise #2
Video Solution
Step-by-Step Solution
To solve the problem of finding what equals, we will apply some rules of logarithms:
Let's work through the solution step-by-step:
- Step 1: Apply the change of base formula.
- Step 2: Simplify the expression using properties of logarithms.
- Step 3: Identify the expression among the given choices.
Now, let's apply the steps:
Step 1: Use the change of base formula.
By the change of base formula, we know that:
for any base . Using the natural logarithm base for simplicity, we substitute into these expressions:
Step 2: Simplify.
Now, multiply the two expressions:
Simplifying, we get:
Step 3: Expression equivalence analysis.
By rearranging the terms using logarithmic properties, it follows that the expression simplifies to:
Therefore, the solution to the problem is .
This matches option 1 in the multiple choice answers provided.
Answer
Exercise #3
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Apply the change of base formula to each logarithm
- Step 2: Multiply the results using properties of logarithms
- Step 3: Simplify the expression to find a matching answer
Now, let's work through each step:
Step 1: Express each logarithm using the change of base formula. Choose base 10 for simplicity:
Step 2: Multiply these two expressions:
Simplifying, we have:
Step 3: Use properties of logarithms to combine numerators and denominators:
The numerator can be written as:
The denominator can be simplified using logarithmic properties:
Since the logarithm of base 10 to its value is 1:
Therefore, the expression becomes:
By simplifying and finding the correct match, we realize that our earlier simplification without taking additional steps directly equates to one of the answers given:
Returning to rewriting using properties of logarithms:
Notice in original expressions and by transforming approach, we recognize identity opportunities coinciding
By analyzing simplification, combine consistent to coefficient approach forms:
The conclusion simplifies:
The solution to the problem is: .
Answer
Exercise #4
Video Solution
Step-by-Step Solution
To solve the expression , we use a known logarithmic property. This property states that:
Applying this property allows us to simplify:
Next, we need to calculate . Since 9 can be expressed as , we have:
Using the power rule of logarithms, , we find:
Since , it follows that:
Therefore, the value of is .
The correct answer choice is therefore Choice 3: .
Answer
Exercise #5
Video Solution
Step-by-Step Solution
To solve this problem, we need to evaluate . We'll use the change of base formula to simplify the logarithms.
- Step 1: Apply the change of base formula to both logarithms.
- Step 2: Simplify the expressions by substituting appropriate values.
- Step 3: Compute the multiplication of the simplified values.
Step 1: Convert the logarithms using the change of base formula:
and .
Step 2: Substitute these back into the expression:
.
Recognize that and , hence simplifying gives:
= .
Step 3: Cancel terms and calculate:
The terms and cancel out:
= .
Therefore, the solution to the problem is , which corresponds to choice 3 in the provided answer choices.
Answer
More Questions
Multiplication of Logarithms
- Solve the Logarithmic Equation: log₃(x²)log₅(27) - log₅(8) = ln(e)
- Solve: log₂(3x) × log₅(8) = log₅(a) + log₅(2a) for Variable X
- Solve Complex Logarithmic Equation: log₅9(log₃4x + log₃(4x+1)) = 2(log₅4a³ - log₅2a)
- Solve Complex Logarithm Equation: Product of Log_a(x), Log_b(y), and Log_c(2)
- Solve Mixed Logarithmic Equation: ln(8x) and log₇(e²) Problem









