Tiling with Regular Polygons

Tiling is essentially covering a surface with tiles of the same type.
In real life, we can encounter tiling in our home or even right in our math notebook.
If we look at the floor in our house, we see identical square tiles covering the entire floor. If we look at our math notebook, we see identical small squares covering the entire page of the notebook.
Tiling can be made up of identical tiles no matter what shape – triangles, circles, and even pentagons.

A regular polygon is a polygon in which all its angles are equal to each other and all its sides are equal to each other.
How can we remember this?
The word "regular" signifies something upgraded and exceptional, so you can remember that this polygon is not just any polygon but one where all its sides are equal and all its angles are equal.
Examples of regular polygons:

Equilateral triangle – a polygon in which all sides are equal and all angles are equal.

Square – all sides are equal and all angles are equal to 90.

Regular pentagon – has 5 equal sides and 5 equal angles.

Now, since we know what tiling is and what a regular polygon is, it's time to connect the two topics!

Tiling with regular polygons is essentially tiling composed of identical regular polygons of one type that "stick" to the edge of the other regular polygon of the same type.
This will create a situation where the sum of the angles at each vertex will be 360!
You can achieve 3 such tilings using – triangles, squares, and hexagons.

Important to know:
• There are no gaps between the polygons
• No polygon covers or overlaps another polygon
• The polygons are adjacent to each other along the entire edge and each vertex touches another vertex
Let's see this in the illustration:

Tiling with Triangles

Tiling with Squares

Tiling with Regular Hexagons

Notice how in all the examples we have seen, the side of one weighted average perfectly adheres to the side of the other weighted average.

And now let's practice!
Determine whether it is a proper tiling of regular polygons –
First example:

Solution:
The answer is a definite no!
Although the tiling is made up of regular polygons, it is not correct! The polygons overlap each other, do not fit perfectly to the sides of the other polygons, and do not connect at the vertices.

Second example:

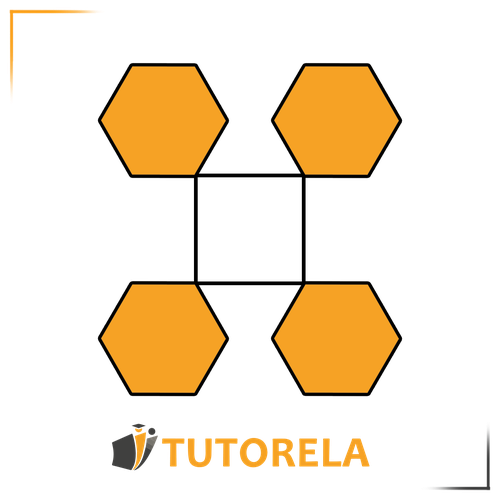
Is this a correct tiling of regular polygons?

Solution –
The answer is definitely not!
In this example, non-identical regular polygons were used – a square and a hexagon.
Additionally, there are gaps between the polygons and they do not fit perfectly together.