The sum of the exterior angles of a polygon will always be degrees, regardless of the polygon.
Sum of the Exterior Angles of a Polygon
What is the external angle of a polygon?
An external, or exterior, angle is the one that is found between an original side of the polygon and its extension.
The angle is located outside of the polygon and hence its name derives.
Let's see it in an illustration
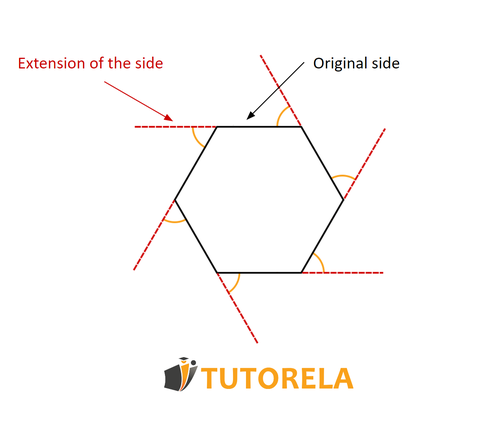
Tip to Know How to Identify an Exterior Angle
Observe only the original sides of the polygon.
Now imagine that, the person who was drawing the polygon fell asleep while doing it, without realizing it they continued outlining one of its sides a little more.
The angle that is created between the original side and the side that was unintentionally continued, is the external angle.
The sum of the external angles of a polygon will always be degrees! In any polygon that is.
Observe, the exterior angle is located between the side that was extended by "falling asleep" and the original side of the polygon.
An angle originated between two sides that were extended by "falling asleep" is not considered an external angle.
For example
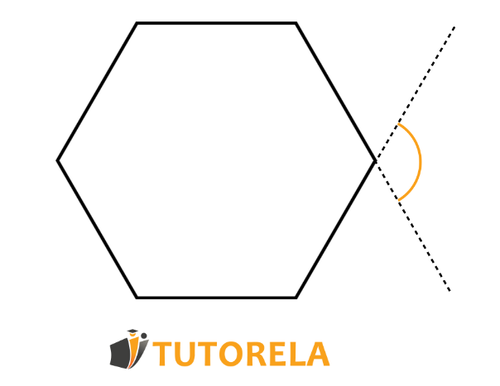
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Midsegment
- Midsegment of a triangle
- Midsegment of a trapezoid
- Sum of the Interior Angles of a Polygon
- Exterior angles of a triangle
- Relationships Between Angles and Sides of the Triangle
- Relations Between The Sides of a Triangle
- Square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- Diagonals of a Rhombus
- Lines of Symmetry in a Rhombus
- From Parallelogram to Rhombus
- Measurement of an angle of a regular polygon
- Angles in Regular Hexagons and Octagons
- Diagonals in a rectangle
- Symmetry in a kite








