Sum of the Interior Angles of a Polygon

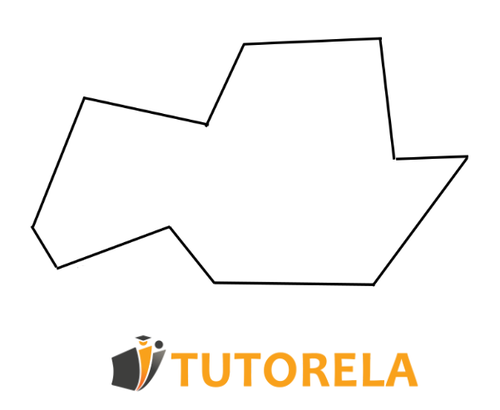
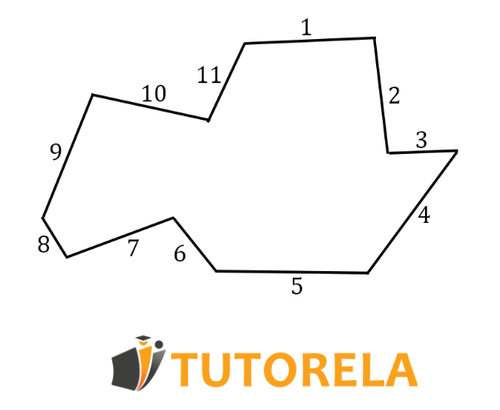
We can very easily calculate the sum of the internal angles of a polygon using the following formula:

When: n= n = number of edges or sides of the polygon


In reality, the sum of all the internal angles of a polygon depends on the number of edges it has.
Steps to follow to find the sum of the internal angles of a polygon:

  1. Count how many sides it has.
  2. Place it in the formula and we will obtain the sum of the internal angles of the polygon.


Pay attention:
In the formula, there are parentheses that require us to first perform the operations of subtraction (first we will subtract 2 2 from the number of edges and only then multiply by 180 180 .)
Regardless of the polygon you have, concave, convex, or regular, thanks to this formula you will be able to find the sum of the internal angles of any polygon.

Let's look at an example

Given the following polygon:  

image 1 Given the following polygon


At first glance, it seems like a very strange polygon that will be difficult to calculate the sum of its internal angles.
But hey!
The formula to calculate the sum of the internal angles of a polygon (of any polygon, even the ones that look weird) is right here and also the steps we must follow
So, let's get to work!
Let's count how many sides our polygon has:

Let's count how many sides our polygon has


Recommendation: Write numbers next to each edge to avoid confusion in the count.

Excellent! Now we know the number of edges our polygon has. n=11n=11
What remains to be done is to place the data in the formula (with caution and preserving the order of mathematical operations)


180(11−2)=180(11-2)=
180∗9=1620180*9=1620

16201620 is the sum of the internal angles of a polygon with 11 11 edges


Useful Information:
all the internal angles of a regular polygon are equal. Therefore, after discovering the sum with the learned formula, you can divide it by the number of angles and arrive at the value of each of the angles.

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Related Subjects