Isosceles Trapezoid Diagonal Properties Practice Problems

Given that the trapezoid is isosceles and the angles on both sides are equal, it can be argued that:

$∢C=∢D$

$∢A=∢B$

We know that the sum of the angles of a quadrilateral is 360 degrees.

Therefore we can create the formula:

$∢A+∢B+∢C+∢D=360$

We replace according to the existing data:

$120+120+2x+2x=360$

 $240+4x=360$

$4x=360-240$

$4x=120$

We divide the two sections by 4:

$\frac{4x}{4}=\frac{120}{4}$

$x=30$

Let's recall that in an isosceles trapezoid, the sum of the two angles on each of the trapezoid's legs equals 180 degrees.

In other words:

$A+C=180$

$B+D=180$

Since angle D is known to us, we can calculate:

$180-50=B$

$130=B$

To solve this problem, we'll follow these steps:

• Step 1: Define the geometric properties of a trapezoid.
• Step 2: Define the geometric properties of an isosceles trapezoid.
• Step 3: Conclude whether an isosceles trapezoid has two pairs of parallel sides based on these definitions.

Now, let's work through each step:
Step 1: A trapezoid is defined as a quadrilateral with at least one pair of parallel sides.
Step 2: An isosceles trapezoid is a special type of trapezoid where the non-parallel sides (legs) are of equal length. Its defining feature is having exactly one pair of parallel sides, which is the same characteristic as a general trapezoid.
Step 3: Since the definition of a trapezoid inherently allows for only one pair of parallel sides, an isosceles trapezoid, as a type of trapezoid, cannot have two pairs of parallel sides. A quadrilateral with two pairs of parallel sides is typically designated as a parallelogram, not a trapezoid.

Therefore, the solution to the problem is that isosceles trapezoids do not have two pairs of parallel sides. No.

True: in every isosceles trapezoid the base angles are equal to each other.

Let's closely examine the properties of an isosceles trapezoid to determine the relationship between its opposite angles.

An isosceles trapezoid is a type of trapezoid where the non-parallel sides (legs) are of equal length. It also implies that the angles adjacent to each leg are equal, due to the symmetry of the trapezoid. However, the most crucial aspect for this problem involves understanding the sum of angles in a trapezoid and their specific relationships.

Consider an isosceles trapezoid, $ABCD$, with base $AB$ parallel to base $CD$, and legs $AD$ and $BC$ being equal.

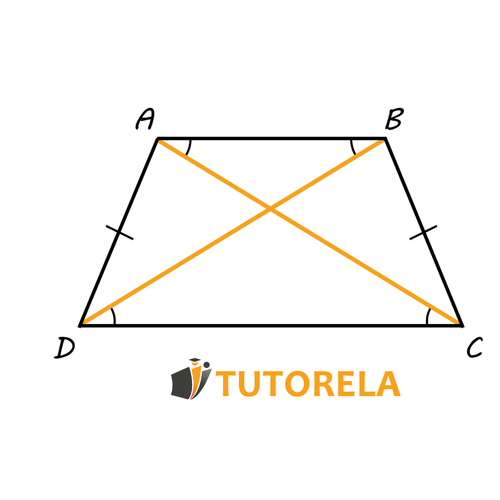
• The key property in any trapezoid is that each pair of angles on the same side of one of the non-parallel sides ($AD$ or $BC$) are supplementary. That is, angles $\angle DAB$ and $\angle ABC$ together sum to $180^\circ$ since they are co-interior angles formed by a transversal cutting the parallel lines $AB$ and $CD$.
• Similarly, angles $\angle BCD$ and $\angle CDA$ also sum to $180^\circ$.

In addition, the total sum of the interior angles of any quadrilateral (and thus any trapezoid) is $360^\circ$. Therefore, opposite angles $\angle DAB$ and $\angle BCD$ (first set) sum to $180^\circ$, and similarly, opposite angles $\angle ABC$ and $\angle CDA$ (second set) also sum to $180^\circ$. Therefore, the sum of the opposite angles in an isosceles trapezoid is always $180^\circ$.

Thus, through application of the properties of parallel lines and angle sums, we find that the sum of opposite angles in an isosceles trapezoid is indeed always $180^\circ$.

The correct conclusion of this problem is that the statement is True.

The sum of the opposite angles in an isosceles trapezoid is always $180^\circ$.