The trapezoid is considered one of the most intimidating shapes for students, therefore we have decided to provide a summary of the general idea behind the trapezoid and explain its properties to them and introduce some types of trapezoids.
Trapezoid Practice Problems for 9th Grade - Area & Properties
Master trapezoid properties, area formulas, and angle calculations with step-by-step practice problems designed for ninth grade students learning quadrilaterals.
📚Master Trapezoid Concepts Through Targeted Practice
- Calculate trapezoid area using the formula with parallel bases and height
- Identify and classify isosceles, right angle, and standard trapezoids
- Find missing angles in isosceles trapezoids using angle properties
- Solve for unknown variables in trapezoid area problems
- Apply midsegment theorem to find missing trapezoid measurements
- Determine ratios between trapezoid segments and triangle areas
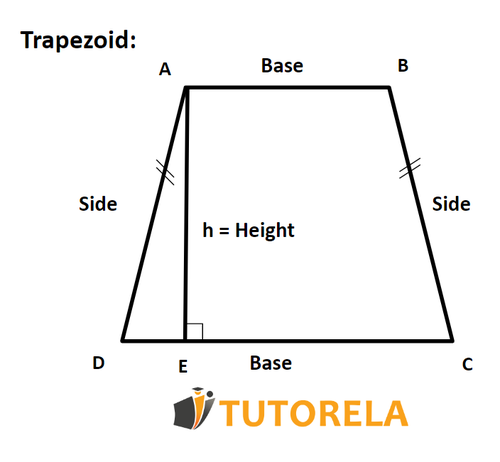
Understanding Trapezoids
Complete explanation with examples
Characteristics of the Trapezoid
A trapezoid is a quadrilateral based on 4 sides like any other,
but special in that it will always have two parallel sides also called bases, which we can call the larger base and the smaller base
and it will also have two opposite sides also called legs.
Practice Trapezoids
Test your knowledge with 41 quizzes
Given the following trapezoid:
Calculate the area of the trapezoid ABCD.
Examples with solutions for Trapezoids
Step-by-step solutions included
Exercise #1
Calculate the area of the trapezoid.
Step-by-Step Solution
We use the formula (base+base) multiplied by the height and divided by 2.
Note that we are only provided with one base and it is not possible to determine the size of the other base.
Therefore, the area cannot be calculated.
Answer:
Cannot be calculated.
Video Solution
Exercise #2
Calculate the area of the trapezoid.
Step-by-Step Solution
To find the area of the trapezoid, we would ideally use the formula:
where and are the lengths of the two parallel sides and is the height. However, the given information is incomplete for these purposes.
The numbers provided (, , , and ) do not clearly designate which are the bases and what is the height. Without this information, the dimensions cannot be definitively identified, making it impossible to calculate the area accurately.
Thus, the problem, based on the given diagram and information, cannot be solved for the area of the trapezoid.
Therefore, the correct answer is: It cannot be calculated.
Answer:
It cannot be calculated.
Video Solution
Exercise #3
Given the trapezoid:
What is its perimeter?
Step-by-Step Solution
The problem requires calculating the perimeter of the trapezoid by summing the lengths of its sides. Based on the given trapezoid diagram, the side lengths are clearly marked as follows:
- First side:
- Second side:
- Third side:
- Fourth side:
According to the formula for the perimeter of a trapezoid:
Substituting the respective values:
Calculating the sum, we find:
Thus, the perimeter of the trapezoid is .
Answer:
32
Video Solution
Exercise #4
What is the perimeter of the trapezoid in the figure?
Step-by-Step Solution
To find the perimeter we will add all the sides:
Answer:
24
Video Solution
Exercise #5
Look at the trapezoid in the figure.
Calculate its perimeter.
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify all given side lengths of the trapezoid.
- Step 2: Apply the formula for the perimeter of the trapezoid.
- Step 3: Sum up the lengths to find the perimeter.
Now, let's work through each step:
Step 1: The problem gives us the lengths of the trapezoid's sides:
-
-
-
-
Step 2: We use the formula for the perimeter of a trapezoid:
Step 3: Plugging in the given values, we calculate:
Calculating further, we have:
Therefore, the perimeter of the trapezoid is .
Answer:
24.2
Video Solution
Frequently Asked Questions
What is the formula for finding the area of a trapezoid?
+The area of a trapezoid is calculated using the formula: Area = (b₁ + b₂) × h ÷ 2, where b₁ and b₂ are the lengths of the parallel bases and h is the height. This formula works by finding the average of the two bases and multiplying by the height.
How do you identify different types of trapezoids?
+There are three main types: 1) Regular trapezoid - has one pair of parallel sides, 2) Isosceles trapezoid - has equal leg lengths and equal base angles, 3) Right trapezoid - contains two right angles where the height equals one of the legs.
What are the angle properties of an isosceles trapezoid?
+In an isosceles trapezoid, base angles are equal (angles on the same base have equal measures), and adjacent angles are supplementary (they add up to 180°). The legs are also equal in length, making it symmetric across its vertical axis.
How do you find missing angles in trapezoids?
+Use these rules: adjacent angles on the same side add to 180°, base angles in isosceles trapezoids are equal, and the sum of all angles equals 360°. Start with known angles and apply these properties systematically.
What is a midsegment in a trapezoid and how do you calculate it?
+A midsegment connects the midpoints of the two legs (non-parallel sides) of a trapezoid. Its length equals the average of the two parallel bases: midsegment = (base₁ + base₂) ÷ 2, and it runs parallel to both bases.
How do you solve trapezoid problems with variables?
+Steps to follow: 1) Identify what the variable represents, 2) Set up the area formula or angle relationship, 3) Substitute known values, 4) Solve the resulting equation algebraically, 5) Check your answer by substituting back into the original problem.
What makes trapezoid problems challenging for 9th graders?
+Students often struggle with: distinguishing between different trapezoid types, remembering that only one pair of sides is parallel, applying the correct area formula, and working with variables in geometric contexts. Practice with labeled diagrams helps overcome these challenges.
How are trapezoids different from parallelograms?
+Key differences: Trapezoids have exactly one pair of parallel sides (bases), while parallelograms have two pairs of parallel sides. In trapezoids, only base angles may be equal (in isosceles type), whereas parallelograms have opposite angles equal and adjacent angles supplementary.