Given: $$ \left|5x + 3\right| \leq 7 $$ Which of the following statements is necessarily true?

$$ x \leq -2 \text{ or } x \geq 0.8 $$

Given: $$ |3x - 2| \geq 4 $$ Which of the following statements is necessarily true?

$$ x \geq 2 $$ or $$ x \leq -\frac{2}{3} $$

$$ \frac{1}{3} < x < \frac{5}{3} $$

Inequalities with Absolute Values - Examples, Exercises and Solutions

Understanding Inequalities with Absolute Values

Complete explanation with examples

Inequality

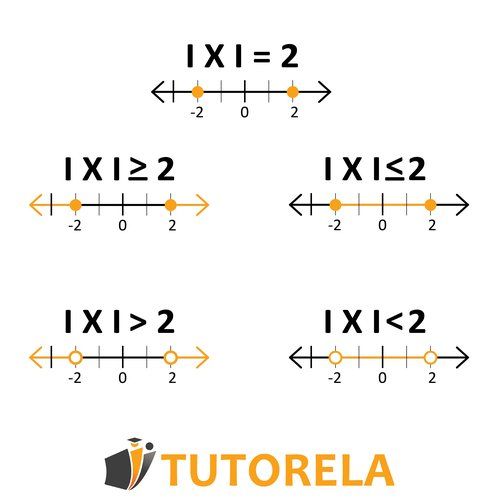
When you come across signs like $<$ or , $>$ , and even $≤$ or $≥$ ,you will know it is an inequality.
Inequalities define ranges of possible values rather than single solutions, whether one value is less than, greater than, or equal to another, helping to describe situations where quantities can vary within certain limits. Therefore, The result of the inequality will be a certain range of values that you will have to find.

An important rule to keep in mind: when you double or divide both sides of the operation, the sign of the inequality is reversed!

Absolute Value Inequality

Absolute value inequality is an inequality that involves the absolute value of a variable or expression. The absolute value represents the distance of a number from zero on the number line, always as a non-negative quantity. In inequalities, this means solving for a range of values that satisfy the given condition, either greater than or less than a certain value, regardless of sign. Absolute value inequalities often split into two cases, one considering the positive side and the other the negative, providing two sets of possible solutions.

Number line visualizations of absolute value equations and inequalities, including |x| = 2, |x| ≥ 2, |x| ≤ 2, |x| > 2, and |x| < 2, with open and closed circles to represent boundary inclusion.

We can solve absolute value inequalities in $2$ ways:

The geometric method

We will draw a number line, and mark the point from which we are interested in the distance to $X$ .
Then we find the points whose distance from the relevant point is exactly the distance mentioned in the condition.
Now, let's pay attention to the condition: $>$ or $<$ And we will find the results.

The algebraic method

Step 1: Divide into two cases:
- Case 1: Assume the expression inside the absolute value is positive.
- Case 2: Assume the expression inside the absolute value is negative.
Step 2: Return to the original inequality:
- Case 1: Remove the absolute value and solve.
- Case 2: Remove the negative sign, solve the inequality.
Step 3: Find the common domain for both cases.
Step 4: Use a number line to mark valid ranges.
Step 5: Determine all values of $X$ that satisfy the inequality.

Detailed explanation

Practice Inequalities with Absolute Values

Test your knowledge with 10 quizzes

Given:

$\left|x-5\right|>11$

Which of the following statements is necessarily true?

Examples with solutions for Inequalities with Absolute Values

Step-by-step solutions included

Exercise #1

Given:

$\left|2x-1\right|>-10$

Which of the following statements is necessarily true?

Step-by-Step Solution

Let's solve the problem:
Step 1: Recognize that the inequality we are dealing with is $\left|2x-1\right| > -10$ .
Step 2: Consider the nature of absolute values: for any real $x$ , $\left|2x-1\right|$ is always non-negative (i.e., $\geq 0$ ).
Step 3: Observe that the right side of the inequality, $-10$ , is negative. Therefore, the inequality $\left|2x-1\right| > -10$ is always true because $\left|2x-1\right|$ as a non-negative quantity will always be greater than any negative number.
Step 4: Since the inequality condition always holds true, this means that the statement is valid for all $x$ .

Therefore, the correct answer is that the inequality holds for all $x$ .

The solution to the problem is For all x.

Answer:

For all x

Video Solution

Exercise #2

Given:

$\left|x-5\right|>-11$

Which of the following statements is necessarily true?

Step-by-Step Solution

The absolute value expression $\left| x - 5 \right| > -11$ inherently suggests that for any real number $x$ , the inequality holds.

Since the absolute value of any expression is always non-negative and $-11$ is negative, the condition $\left| x - 5 \right| > -11$ is always satisfied regardless of the choice of $x$ .

Thus, there is no specific limitation or exceptional circumstance that confines $x$ to any particular subset of the real numbers.

This implies that no particular statement about $x$ being greater, less, or constrained to a specific domain can be justified. Therefore, the notion of any statement being "necessarily true" in the conventional sense of constraining $x$ does not apply.

The correct answer, therefore, is: all $x$ .

Answer:

all $x$

Video Solution

Exercise #3

Solve the inequality:

$|2x - 5| > 7$

Step-by-Step Solution

To solve $|2x - 5| > 7$ , we consider the definition of absolute value inequality $|A| > B$ , which means $A > B$ or $A < -B$ .

Thus, $2x - 5 > 7$ or $2x - 5 < -7$ .

Let's solve these inequalities separately:

1. $2x - 5 > 7$

Add 5 to both sides:

$2x > 12$

Divide by 2:

$x > 6$

2. $2x - 5 < -7$

Add 5 to both sides:

$2x < -2$

Divide by 2:

$x < -1$

Therefore, the solution is $x < -1 \text{ or } x > 6$ .

Answer:

$x < -1 \text{ or } x > 6$

Exercise #4

Given:

$\left|2x + 1\right| > 3$

Which of the following statements is necessarily true?

Step-by-Step Solution

To solve $\left| 2x + 1 \right| > 3$ , consider the two cases for the absolute value: $2x + 1 > 3$ and $2x + 1 < -3$ .

1. Solving $2x + 1 > 3$ :

$2x + 1 > 3$

Subtract 1 from both sides:

$2x > 2$

Divide both sides by 2:

$x > 1$

2. Solving $2x + 1 < -3$ :

$2x + 1 < -3$

Subtract 1 from both sides:

$2x < -4$

Divide both sides by 2:

$x < -2$

Thus, the solution is $x < -2 \text{ or } x > 1$ .

Answer:

$x < -2 \text{ or } x > 1$

Exercise #5

Given:

$\left|3x - 4\right| \leq 5$

Which of the following statements is necessarily true?

Step-by-Step Solution

To solve $\left| 3x - 4 \right| \leq 5$ , we should consider two scenarios for the absolute value: $3x - 4 \leq 5$ and $3x - 4 \geq -5$ .

1. Solving $3x - 4 \leq 5$ :

$3x - 4 \leq 5$

Add 4 to both sides:

$3x \leq 9$

Divide both sides by 3:

$x \leq 3$

2. Solving $3x - 4 \geq -5$ :

$3x - 4 \geq -5$

Add 4 to both sides:

$3x \geq -1$

Divide both sides by 3:

$x \geq -\frac{1}{3}$

Combining both results, we have $-\frac{1}{3} \leq x \leq 3$ , which is the correct answer.

Answer:

$-\frac{1}{3} \leq x \leq 3$

Continue Your Math Journey

Master Inequalities with Absolute Values first, then advance to these related topics that build on your fraction skills

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Double absolute value Solving the problem

Inequalities with Absolute Values - Examples, Exercises and Solutions

Understanding Inequalities with Absolute Values

Inequality

Absolute Value Inequality

We can solve absolute value inequalities in $2$ ways:

The geometric method

The algebraic method

Practice Inequalities with Absolute Values

Examples with solutions for Inequalities with Absolute Values

More Inequalities with Absolute Values Questions