Key Metrics in Statistics

Frequency - as the name implies. It is the recurring value in a particular data list with the highest frequency. There may also be cases where there is more than one frequency.
Average - is calculated by dividing the sum of all the data by the number of data. It is important to note that the average will always lie between the maximum and minimum value of the data. The average does not have to be a whole number nor does it have to appear in the list of data.
Median - is the middle value within an ascending or descending list of data. This means that fifty percent of the data will be greater than the median and fifty percent of the data will be less than the median. When the list of data has an even number of elements, the median need not be one of the data in the list.

We will illustrate the concept of frequency by using an example

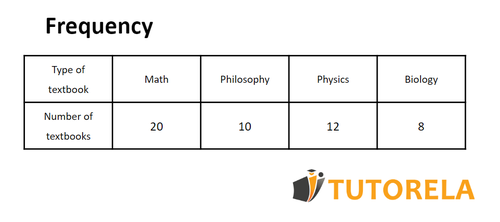
Below is a table illustrating the distribution of study books according to subject. There are a total of $50$ study books.

We are asked to find the most frequent type of study books. How many times does it appear?

Let's look at the table, and it appears that the most frequent type of study book is math books. $20$ study books are math books.

Coral bought three pants at the following prices: $ $150$ , $ $80$ and $ $100$ .

We are asked to calculate the average price Coral paid for a pair of pants.

Calculate the average price by applying the rule we learned about calculating averages: divide the sum of all the data by the number of data.

The sum of all the data is: $150+80+100=330$ $.

The number of data is $3$ (a total of 3 pants).

Now we get: average $=\frac{330}{3}=110$ $.

That is, the average price Coral paid for a pair of pants is $ $110$ . You can see that the average itself does not appear at all in the data list.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

List of data:

$10,30,50,70,90$

We must find the median.

This is a list of numbers sorted in ascending order (otherwise we would have to sort them ourselves).

The number $50$ is in a central position, since we refer to an odd number of elements ( $50$ ).

Therefore, the median is $50$ .

List of data:

$10,30,50,70,90,110$

We must find the median.

This is a list of numbers sorted in ascending order (otherwise we would have to sort them ourselves).

This time we refer to an even number of elements ( $6$ ), so we have two main elements: $50$ and $70$ .

To calculate the median, we must calculate the average of the two central numbers.

We obtain: median $=\frac{(50+70)}{2}=\frac{120}{2}=60$

That is, in this case the median is $60$ .

It is important to note that the median does not have to be one of the data in the list.

If you are interested in this article you may also be interested in the following articles:

On the Tutorela blog you will find a variety of articles about mathematics.