Estimation

Given the two expressions $13+65$ and $17+68$

We are asked to determine which expression is greater without solving them.
Upon observing them, we see that $17$ is larger than $13$ and also $68$ is larger than $65$.
If each term of the second expression is greater than those of the first, then the entire second expression is greater than the first.
Therefore, it is true that:

$13+65 < 17+68$

If we know that $600\times 12=7200$
what will be the result of the exercise $12\times 1200$ without calculating it?
Let's look at the data we have and compare it with the exercise we need to solve:

$12\times 1200= 12\times 600\times 2= 7200\times 2= 14400$

In fact, what did we do? In the required exercise, we can represent the $1200$ by $600\times 2$. This will give us the given expression, and all we have to do is multiply the result by $2$.

We can also talk about estimation when referring to percentages.
We will demonstrate this with an example.

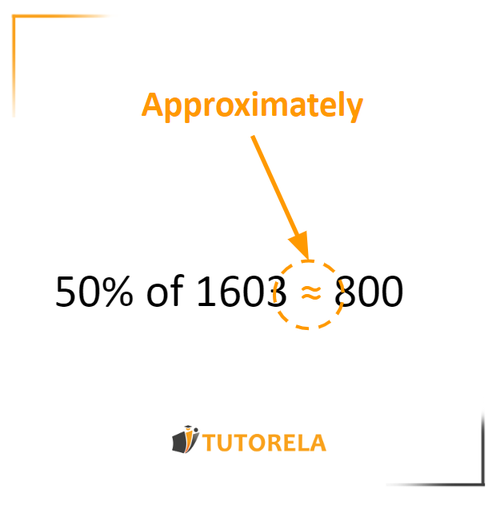
If we need to estimate the $50\%$ of $1503$, we can say that $1503$ is quite close to $1500$, and therefore, we can say that the $50\%$ would give us approximately $750$.

That is, $50\%$ of $1503 ≈ 750$

We need to fill in the greater than/less than/equal to sign between the following two expressions: $69+27$ --- $66+24$

Solution: 

Let's look at the two expressions and see that $69$ is larger than $66$ and also $27$ is larger than $24$.

Therefore, it is not necessary for us to calculate the exact result to determine that:

$69+27 > 66+24$

We are asked to deduce from the following data $40\times 12= 480$ the result of the exercise $40\times 24$.

Solution: 

In this case as well, we can see that $24\times 40=12\times 40\times 2$ holds true.

This means that we do not need an exact calculation, but all we need to do is to multiply the given result by $2$.

Which will give us: $24\times 40=12\times 40\times 2= 480\times 2= 960$

We are asked to solve the exercise $21\times 41$ approximately, without a calculator and without performing an exact calculation.

Solution

In this case too, we can use estimation to make an approximate calculation.

We will round $41$ to $40$.

We will round $21$ to $20$.

Now we will multiply the estimated results and obtain the following: $40\times 20= 800$.

That is, the approximate result of the required exercise is $800$.

If the number $400$ is increased by a number greater than $70$

What can we say about the result?

Solution: 

In this case, it's about adding or subtracting inexact numbers. 

If we add $400$ plus $70$, the result would be $470$.

Since we are adding to $400$ a number larger than $70$, the result we will obtain will be greater than $470$. 

What is estimation in mathematics?

In mathematics, an estimation is an approximation of a calculation, whether it be addition, subtraction, multiplication, or any other operation; however, when estimating, it is not necessary to perform the operation as such, that is, it is not necessary to carry it out and get the exact result, but rather just to estimate an approximate result.

What is an estimation and why is it important?

As we have already mentioned, an estimation is an approximation of some result. It is very important because from a young age we are taught to perform some mental calculations of operations to reach an approximate result without the need to perform the operation as such. As this skill develops, the result will become more precise, that is, closer to the real value.

How do you estimate the result of an operation?

Let's look at some examples of how to estimate the results of some operations

• Estimation of a sum:

Example 1

Prompt. Estimate the result of $142+256=$

Solution

Let's break down the numbers of each addend into hundreds, tens, and ones as follows:

$142=100+40+2$

$256=200+50+6$

Now let's add the hundreds, tens, and ones separately

$100+200=300$

$40+50=90$

$2+6=8$

From here we can estimate that the result will be $398$

Result

$398$

• Estimation of a product

Example 2

Prompt. Estimate the following operation $19\cdot23=$

Solution:

To estimate the result, we will round each factor as follows

The number $19$ will be rounded to $20$

And the number $23$ will be rounded to $20$

Therefore, we perform the multiplication $20\cdot20=400$

Then an approximate result is $400$, it should be noted that this is not the correct result, it is just an estimation of the result.

Result

The estimation is $400$