Probability is the possibility of arriving at a certain outcome.
Probability for 9th Graders
Probability of Independent Random Events
In independent random events, each of the events do not influence the probability of the others.
Representation of Independent Random Events
Independence is denoted as
the independence between random events is denoted as:
Probability is denoted with the letter
Formula to calculate the probability of independent random events:
The meaning of
The probability that the random events and occur at the same time.
Double-entry table to find the solution to probability questions
In the table, there will be two columns and two rows.
First column
will indicate the probability that the first event has occurred
Second column
will indicate the probability that the first event has not occurred
First row
will indicate the probability that the second event has occurred
Second row
will indicate the probability that the second event has not occurred
Inside the table, the probabilities of both events will be shown respectively.
Note: The probability that a certain random event occurs plus the probability that it does not occur, will always result in as a result.
Probability Calculation with Area in a Double Entry Table
Just like a double-entry table, it will consist of two columns and two rows.
We will note next to each column and row the corresponding probability.
The calculation of the area of the square will indicate the probability of both the event indicated in the length and the one indicated in the width occurring.
As the formula for the calculation says, we will multiply the length by the width to obtain the desired probability.
Probability Calculation with Dendrogram (Tree Diagram)
The dendrogram describes the process carried out in the experiment.
Let's draw two branches that describe the probability that the first event occurred and the probability that the first event did not occur.
From the branches we draw, let's draw another pair of branches from each that describe the probability that the second event occurred and the probability that the second event did not occur.
To find the probability that describes what has occurred in the first event and also what has occurred in the second, we will multiply the corresponding probabilities represented on the branches.
Dependent Random Events
In dependent random events, each event influences the probability of occurrence of the other.
Conditional Probability
Conditional probability refers to the case where we have some data that could modify the probability of a certain event having occurred.
Probability
Before we start talking about the probability of independent random events, the probability of dependent random events, and conditional probability, let's remember what probability itself is.
What is probability?
Probability is the possibility of obtaining a specific outcome.
In fact, you can replace the word probability with possibility and arrive at the same meaning.
Probability of Independent Random Events
What are independent random events?
Independent random events are events that occur without being affected by other events. No event influences the probability of another event occurring or not. In fact, we can say in very simple language, that the occurrence of a certain event does not influence the possibility of another event occurring since they do not depend on each other.
There are many examples from daily life where we can observe these types of independent random events, for example:
First event – it rained
Second event – a was rolled on the die
We can say, with absolute certainty, that there is no relationship between it having rained and a being rolled on the die.
The symbol for independent random events is
If we wish to indicate that events and are independent, we will denote it as follows:
Probability we will write with the letter
The probability of independent random events is equal to the product of the probabilities of the two separate events. That is, the probability of event times the probability of event .
Let's see it in the formula:
The meaning of
The probability that the independent random events and occur at the same time.
For example, if the probability of the first event occurring, raining, is
and the probability of the second event occurring, rolling a on the die, is
then, the probabilities of both events together are:
Observe, in questions where it is described that something is taken out and then that something is returned, the events tend to be independent.
If a case is described in which a ball is removed and then returned, in reality, we are returning to the starting point, so the first event does not affect the second.
Let's see an example of questions of this type:
There are balls in a drawer. of them are red and blue.
Dora takes a ball out of the drawer and then returns it. Later she takes out a ball again.
What is the probability that Dora has taken out two blue balls?
Solution:
We will divide the experiment into two events:
The first event - Taking out the blue ball for the first time.
The calculation for this event to occur will be:
There are blue balls among the in the drawer.
Therefore, the probability of taking out a blue one the first time is .
The second event - Taking out the blue ball for the second time.
Also now there are blue balls among the in the drawer since the first was returned.
Therefore, the probability of taking out a blue ball the second time is also .
To discover the probability of these two independent events occurring,
we will multiply the probabilities we obtained according to the formula and we will get:
Different Ways to Calculate the Probability of Independent Random Events
Double-entry table
Double-entry table for solving probability questions:
Do not fear it. It simply represents the data in a clearer and simpler way.
The table will be composed of two columns indicating the probability that the first event has occurred and the probability that the first event has not occurred, and two rows describing the probability that the second event has occurred and the probability that the second event has not occurred.
Inside the table, the probabilities for both events will be seen respectively (for example, one occurred and the other did not)
It is necessary for you to know that the probability of a certain event occurring plus the probability of that event not occurring will always be .
Now, we will describe an excellent example for the use of the double-entry table so you can understand it better:
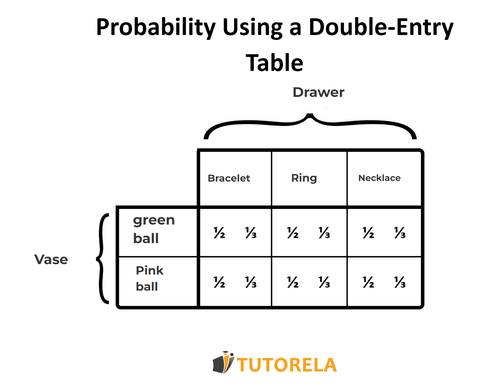
In a vase, there are balls - one pink and the other green.
In a totally different box, which has no relation to the vase, there are three jewels - a ring, a bracelet, and a necklace.
Diana randomly chooses a ball from the vase and then reaches into the box and pulls out a jewel.
We will note in the double-entry table all the possibilities of taking out the ball and taking out the jewel and the probabilities.
Additionally, we will determine how many possibilities exist.
| Cajón / jarrón | Green ball | Pink ball | It seems like you haven't provided any text for translation. Could you please provide the text you need translated? |
| Ring | ring and pink ball | ring and green ball | |
| Brazalete | bracelet and pink ball | bracelet and green ball | |
| Collar | collar and pink ball | collar and green ball | |
| It seems like you haven't provided any text for translation. Could you please provide the text you need translated? |
In the table, we see that there are possible outcomes.
If we were asked the probability of a specific possibility occurring, we could easily respond.
For example, if we are asked about the probability of getting a pink ball and a piece of jewelry worn on the hand –>
it seems there are two options: a ring and pink ball or a bracelet and pink ball.
Therefore, the probability will be: .
That is, 2 options out of the 6 possibilities that exist.
Now we will move on to the second way:
Area in a double-entry table
Calculating probability with area is very similar to calculating with a double-entry table, but it makes us observe the probabilities more closely.
If we look at the table above, we will see that the calculations we note in each segment are the calculation of the area.
Let's see it in a simpler example and calculate the area within the table:
In reality, what we will do is note next to each length and width the corresponding probability.
The calculation of the area of the square in question will indicate the probability that both the event indicated in the length and the one indicated in the width occur.
As in the calculation formula, we will multiply the length by the width and obtain the desired probability.
If, for example, we want to calculate the probability of drawing the bracelet and the green ball, we will get a probability of:
Now we will move on to the third way:
Through a dendrogram (tree diagram)
The dendrogram is a very nice diagram through which we describe the probabilities of each event.
The tree describes in a wonderful way the sequences of the experiment.
First, we will draw two branches that describe the probability that the first event has occurred and the probability that the first event has not occurred.
From the branches we have drawn, we will draw from each of them another pair of branches that describe the probability that the second event has occurred and the probability that the second event has not occurred.
Let's go back to the example of the balls from the first question:
In the drawer, there are balls of them are red and blue.
Dora takes a ball out of the drawer and then returns it. Later, she takes out a ball again.
What is the probability that Dora took out two blue balls?
Let's draw the first outcome and the probabilities of drawing a blue or red ball:
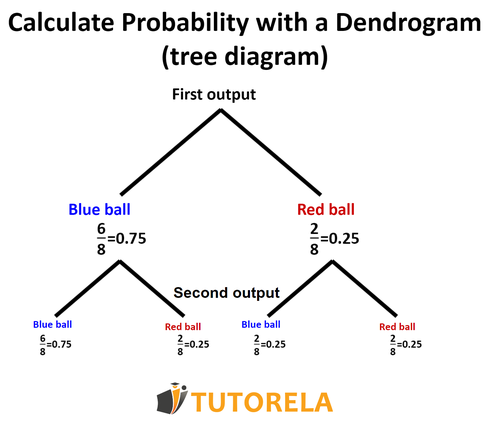
Now, let's continue drawing the second outcome for each branch
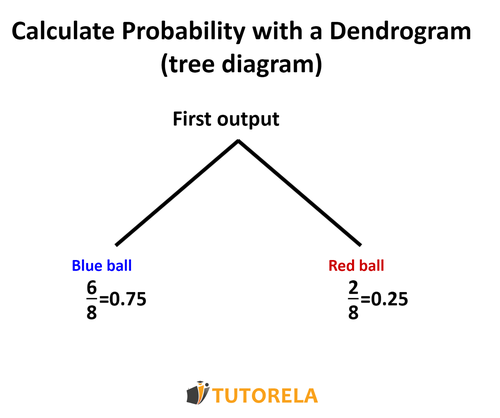
First outcome
Now, when we are asked about the probability of drawing one or the other, we know that all we have to do is multiply the corresponding probabilities.
For example, if we are asked, what is the probability of drawing a blue ball the first time and a red ball the second?
Let's look at the tree,
let's see, what is the probability of drawing a blue ball first? .
Now we need the probability of drawing a red ball second, after drawing a blue one.
Therefore, we will go to the left branch, the branch of the outcome of the blue ball on the first attempt and see that the probability of drawing a red ball on the second attempt is .
We will multiply both probabilities and obtain
Dependent Random Events
Dependent random events are events in which there is some relationship between the probability of the first event occurring and the probability of the second event occurring.
We can perceive that these are dependent random events if we are presented with problems that describe an object being taken out but not returned, then a change occurs that alters the second event.
Likewise, if we are presented with problems of this style: if something were to happen, then something else would happen as a result of the first event, we will know that it is about conditional probability.
Indeed, when we identify dependence between events we will understand that they are dependent events.
An example of dependent random events taken from everyday life is:
First event - Roni studied for the exam
Second event - Roni passed the exam
Our logic should alert us that there is some relationship between these two events. Whether one studies for the exam or not influences whether we will pass the exam or not.
In dependent random events, the dendrogram helps to understand the dependence through the roots and to calculate the correct probability.
Conditional Probability
Conditional probability refers to the case where we have some data that could modify the probability that a certain event has occurred.
Example from everyday life
If we were asked, "What is the probability that it will rain tomorrow in the Land of Oz?"
we wouldn't know how to answer.
But, if we were provided information that it hardly ever rains in the Land of Oz, the probability we would present would be different.
Let's look at a slightly more advanced example
In the fourth grade of a school, there are boys and girls.
girls.
boys.
Some of the students in the class participate in a computer science course and others do not.
study computer science.
do not study computer science.
More data
boys in the class study computer science.
and girls in the class study computer science.
Let's organize the data in the table:
| Total | They do not participate in the computer science course | Participate in the computer science course | It seems like you haven't provided any text for translation. Could you please provide the content you need to be translated from Spanish to English? |
| 15 | therefore there will be 5 | 10 | children |
| 25 | therefore there will be 8 | 17 | girls |
| 40 | 21 | 19 | total |
Now, if we were asked about the probability of randomly picking a male student from the class who is one of those participating in the computer science course, we can look at the table and see that ( 10 \)
boys study computer science out of the ( 15 \) boys in the class and, therefore, the probability will be:
The key to success in conditional probability exercises is to identify the data we know.
Did we select a boy?
Did we select a girl?
or maybe we simply selected participants of the computer science course?
What we know will be in the denominator.
What we do not know will be in the numerator and will mean the part within the data we know.
If you are interested in this article, you might also be interested in the following articles:
Probability of Independent Random Events
In the blog of Tutorela you will find a variety of articles about mathematics.








