Calculate Slope: Finding the Rate Between Points (0,0) and (-8,2)

Q: Why is my slope negative when one point is at the origin?

The slope is negative because the line goes downward from left to right. Even though (0,0) is at the origin, the other point (-8,2) is to the left and up, creating a negative slope of $ -\frac{1}{4} $.

Q: Does it matter which point I call (x₁, y₁)?

No, it doesn't matter! You can choose either point as your starting point. Just make sure to stay consistent - if you pick (-8,2) as (x₁, y₁), then (0,0) must be (x₂, y₂).

Q: What does a slope of -1/4 actually mean?

A slope of $ -\frac{1}{4} $ means for every 4 units you move right, the line drops down 1 unit. The negative sign indicates the line is decreasing.

Q: Can I simplify 2/-8 differently?

Yes! $ \frac{2}{-8} = \frac{-2}{8} = -\frac{2}{8} = -\frac{1}{4} $. All of these are equivalent, but $ -\frac{1}{4} $ is the simplest form.

Slope Calculation with Negative Coordinates

What is the slope of a straight line that passes through the points $(0,0),(-8,2)$ ?

❤️ Continue Your Math Journey!

We have hundreds of course questions with personalized recommendations + Account 100% premium

Step-by-step video solution

Watch the teacher solve the problem with clear explanations

00:06 Let's find the slope of the graph.

00:15 We'll use two points to determine the slope.

00:21 Use the formula for slope. Plug in the values from the two points.

00:28 Substitute the values given, and solve for the slope.

00:40 Now, factor eight into four times two.

00:45 This is the slope of the graph!

00:51 And that's how we solve the problem. Great job!

Step-by-step written solution

Follow each step carefully to understand the complete solution

Understand the problem

What is the slope of a straight line that passes through the points $(0,0),(-8,2)$ ?

Step-by-step solution

To solve the problem, remember the formula to find the slope using two points

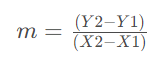
Now, we replace the given points in the calculation:

$\frac{(0-2)}{(0-(-8)}=\frac{-2}{8}=-\frac{1}{4}$

Final Answer

$-\frac{1}{4}$

Key Points to Remember

Essential concepts to master this topic

Slope Formula: Use m = (y₂ - y₁)/(x₂ - x₁) for any two points
Technique: Calculate $\frac{2-0}{-8-0} = \frac{2}{-8} = -\frac{1}{4}$
Check: Verify by plotting points and confirming line falls left to right ✓

Common Mistakes

Avoid these frequent errors

Confusing coordinate order in slope formula
Don't mix up which point is (x₁, y₁) and which is (x₂, y₂) = wrong sign! This changes positive slopes to negative or vice versa. Always keep coordinates paired: if you use y₂ first, use x₂ first too.

Practice Quiz

Test your knowledge with interactive questions

What is the solution to the following inequality?

$$ 10x-4\leq-3x-8 $$

FAQ

Everything you need to know about this question

Why is my slope negative when one point is at the origin?

The slope is negative because the line goes downward from left to right. Even though (0,0) is at the origin, the other point (-8,2) is to the left and up, creating a negative slope of $-\frac{1}{4}$ .

Does it matter which point I call (x₁, y₁)?

No, it doesn't matter! You can choose either point as your starting point. Just make sure to stay consistent - if you pick (-8,2) as (x₁, y₁), then (0,0) must be (x₂, y₂).

How do I handle the negative coordinate in (-8,2)?

Treat negative coordinates just like regular numbers in the formula. Remember: subtracting a negative becomes addition! So 0 - (-8) = 0 + 8 = 8.

What does a slope of -1/4 actually mean?

A slope of $-\frac{1}{4}$ means for every 4 units you move right, the line drops down 1 unit. The negative sign indicates the line is decreasing.

Can I simplify 2/-8 differently?

Yes! $\frac{2}{-8} = \frac{-2}{8} = -\frac{2}{8} = -\frac{1}{4}$ . All of these are equivalent, but $-\frac{1}{4}$ is the simplest form.

🌟 Unlock Your Math Potential

Get unlimited access to all 18 Linear Functions questions, detailed video solutions, and personalized progress tracking.

📹

Unlimited Video Solutions

Step-by-step explanations for every problem

📊

Progress Analytics

Track your mastery across all topics

🚫

Ad-Free Learning

Focus on math without distractions

No credit card required • Cancel anytime