Determine the Sign: Solving (-2)×(-4) Multiplication Problem
Integer Multiplication with Negative Numbers
What will be the sign of the result of the next exercise?
❤️ Continue Your Math Journey!
We have hundreds of course questions with personalized recommendations + Account 100% premium
Step-by-step video solution
Step-by-step written solution
Understand the problem
What will be the sign of the result of the next exercise?
Step-by-step solution
It's important to remember: when we multiply a negative by a negative, the result is positive!
You can use this guide:
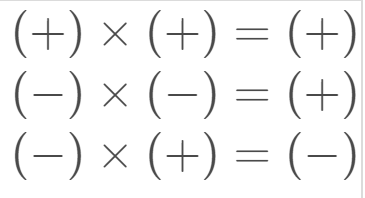
Final Answer
Positive
Key Points to Remember
- Sign Rule: Negative times negative always equals positive
- Technique: because signs are same
- Check: Count negative signs: two negatives make one positive ✓
Common Mistakes
- Thinking negative times negative equals negative Don't assume (-2) × (-4) = -8 because you see negative numbers! This ignores the fundamental sign rule and gives the opposite answer. Always remember: same signs (both negative) multiply to give positive results.
Practice Quiz
Solve the following exercise:
\( (+6)\cdot(+9)= \)
FAQ
Why does negative times negative equal positive?
+Think of it as "opposite of opposite" - when you reverse a reversal, you get back to positive! It's like taking away a debt, which actually gives you money.
How can I remember the sign rules for multiplication?
+Use this simple pattern: Same signs = Positive, Different signs = Negative. So (+)(+) and (-)(-) are positive, while (+)(-) and (-)(+) are negative.
What if I have more than two negative numbers?
+Count the negative signs! An even number of negatives gives positive, an odd number gives negative. For example: (-2)(-3)(-4) has 3 negatives (odd), so the result is negative.
Does this rule work for division too?
+Yes! The same sign rules apply to division. Negative ÷ Negative = Positive, just like multiplication. For example: (-8) ÷ (-2) = +4.
How do I solve this without a calculator?
+First ignore the signs and multiply: 2 × 4 = 8. Then apply the sign rule: since both numbers are negative, the answer is positive, so .
🌟 Unlock Your Math Potential
Get unlimited access to all 18 Signed Numbers (Positive and Negative) questions, detailed video solutions, and personalized progress tracking.
Unlimited Video Solutions
Step-by-step explanations for every problem
Progress Analytics
Track your mastery across all topics
Ad-Free Learning
Focus on math without distractions
No credit card required • Cancel anytime