Every geometric problem is based on data, and the solution is divided into several different questions. One of the most popular questions, and the one most likely to appear on your test, is the question about the area of a rhombus. As is well known, a rhombus consists of different triangles. If so, how do you calculate its area?
Area of a Rhombus Practice Problems - Diagonal & Base Height
Master rhombus area calculations with step-by-step practice problems using diagonal formulas and base-height methods. Includes worked examples and solutions.
- Calculate rhombus area using diagonal multiplication formula: (d1 × d2) ÷ 2
- Apply base times height formula for rhombus area problems
- Solve for missing diagonals when area is given
- Use Pythagorean theorem to find unknown diagonal lengths
- Work with rhombus ratio problems and diagonal relationships
- Convert between different rhombus area calculation methods
Understanding Area of a Rhombus
How is the area of a rhombus calculated?
Rhombus Formula
- The formula to calculate the area of a rhombus: Diagonal Diagonal, divided by .
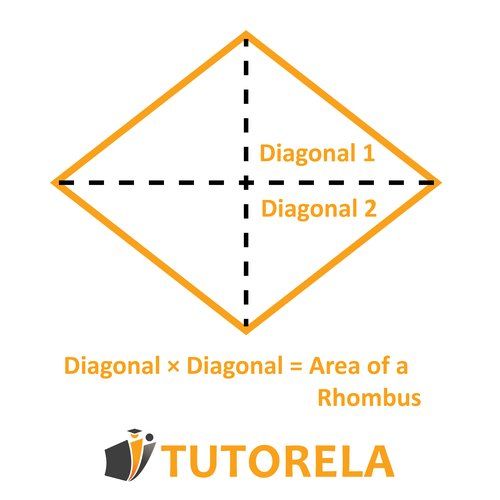
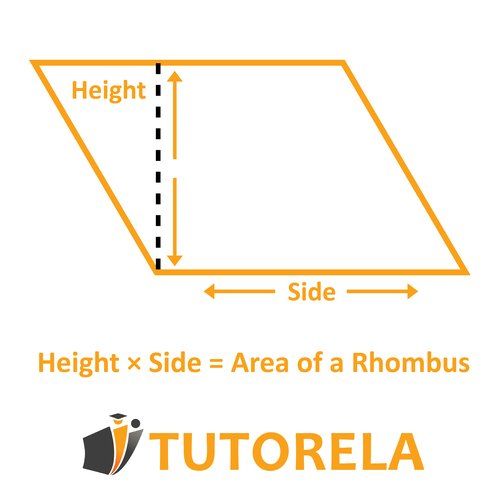
- Another formula you can think of for the area of a rhombus (depending on the information provided by the question): Base Height.
Practice Area of a Rhombus
Look at the rhombus in the figure.
What is its area?
Examples with solutions for Area of a Rhombus
Given the rhombus in the drawing:
What is the area?
Let's remember that there are two ways to calculate the area of a rhombus:
The first is the side times the height of the side.
The second is diagonal times diagonal divided by 2.
Since we are given both diagonals, we calculate it the second way:
Answer:
14
Look at the rhombus in the figure.
What is its area?
First, let's remember that according to the properties of a rhombus, all sides of a rhombus are equal,
Therefore, if we define the sides of the rhombus with the letters ABCD,
We can argue that:
AB=BC=CD=DA
We use the perimeter formula:
50 = AB+BC+CD+DA
And we can conclude that
4AB=50
(We can also use any other side, it doesn't matter in this case because they are all equal.)
We divide by four and reveal that:
AB=BC=CD=DA = 12.5
Now let's remember the formula for the area of a rhombus: the height times the side corresponding to the height.
We are given the length of the external height 8,
Now, we can replace in the formula:
8*12.5=100
Answer:
100 cm²
Using the rhombus in the drawing:
Calculate the area?
Remember there are two options to calculate the area of a rhombus:
1: The diagonal multiplied by the diagonal divided by 2.
2: The base multiplied by the height.
In the question, we are only given the data for one of the diagonals and one of the sides, which means we cannot use either of the above formulas.
We need to find more data. Let's begin by finding the second diagonal:
Remember that the diagonals of a rhombus are perpendicular to one another, which means that they form a 90-degree angle.
Therefore, all the triangles in a rhombus are right-angled.
Now we can focus on the triangle where the side and the height are given, and we will calculate the third side using the Pythagorean theorem:
Insert the given data:
Now that we have found the second half of the diagonal, we can calculate the area of the rhombus by multiplying the two diagonals together.
Since the diagonals in a rhombus are perpendicular and cross each other, they are equal. Hence, our diagonals are equal:
Therefore, the area of the rhombus is:
Answer:
24
A rhombus and its external height are shown in the figure below.
The length of each side of the rhombus is 5 cm.
What is its area?
Answer:
15 cm².
Given the rhombus in the drawing:
What is the area?
Answer:
33