What's its name? Rhombus, kite, or diamond? ;)
Rhombus, kite, or diamond?
Rhombus, Kite, or Diamond? The properties, the formulas, and absolutely everything you need to know
Between us... it doesn't matter. It's about that mysterious geometric figure that reminds us of a precious diamond or a deck of cards... Whatever you call it, you must know the properties of this figure and its uniqueness to solve certain geometric problems.
Rhombus

A rhombus is a polygon with four sides of equal length. Its key properties include:
- All sides have equal length:
- Opposite sides are parallel
- Opposite angles are equal
- The diagonals are perpendicular to each other
Area of a rhombus
there are two ways to find the area of a rhombus:
- The lengths of the diagonals are multiplied and divided by .
- One of the sides is multiplied by the height.
Test yourself on rhombus for ninth grade!
Look at the rhombus in the figure.
What is the relationship between the marked angles?
Definitions of the Rhombus
A rhombus is a polygon with four sides of equal length. If we talk about the "extended family," we can admit that a rhombus is, in fact, a particular case of the figures kite and parallelogram. On the other hand, if a certain rhombus is also characterized by having four equivalent angles (that is, each of 90º) the rhombus becomes a square.
Properties of a Rhombus
Below are the main characteristics that describe a rhombus. To explain them clearly, we will use the following illustration:
Properties of a rhombus
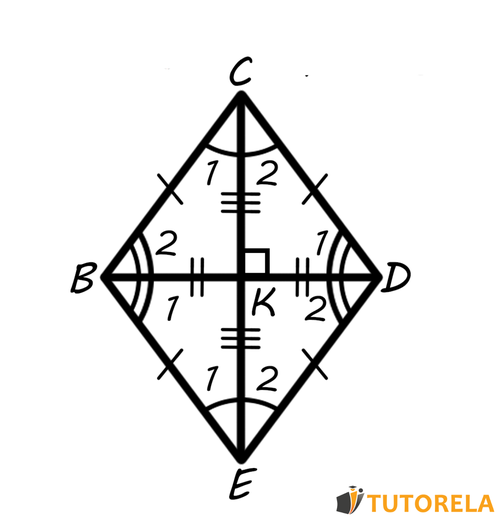
- All sides of the rhombus have the same length. That is:
- The opposite sides of the rhombus are parallel. That is:
- The opposite angles of the rhombus have the same amplitude. That is:
- If a height is measured from each vertex, all four will have the same length. In the illustration, a single height is seen descending from the vertex to the side .
- A circle can be inscribed in any rhombus.
- In every rhombus, there are two perpendicular diagonals. That is: is perpendicular to .
- The meeting point of the two diagonals divides each diagonal into two equal parts. That is:
- Each diagonal divides the angles of the rhombus into two equal angles. That is:
Given the rhombus in the figure
What is your area?
Given the rhombus in the figure
What is your area?
In the drawing given a rhombus
The length of each side of the rhombus is 5 cm
The length of the height of the side is 3 cm
What is the area of the rhombus?
Demonstration of the Rhombus
To demonstrate that a quadrilateral is a rhombus we can use the direct or indirect method. If we opt for the direct method, we must prove that the four sides of said quadrilateral have the same length. Using the indirect method, we must first demonstrate that the polygon is a parallelogram. After having managed to prove that a certain quadrilateral is a parallelogram, we are left with three options:
- Prove that the diagonals of the parallelogram act as bisectors
- Prove that the diagonals of the parallelogram are perpendicular
- Prove that the two adjacent sides of the parallelogram are equivalent
Depending on the data available in the exercise, we can choose the most appropriate method to act and thus demonstrate that a certain parallelogram is, in fact, a rhombus.
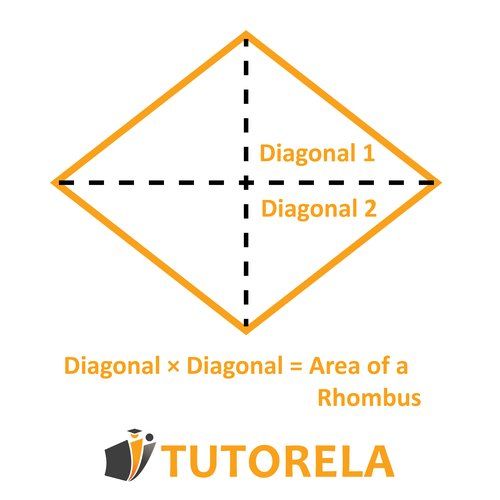
Formula to calculate the area of a rhombus
There are several ways to calculate the area of a rhombus. In this section, we will briefly mention two formulas to calculate the area of the rhombus. If you want to expand your knowledge on the subject, we invite you to read the full article about the area of the rhombus.
To see it in a simple way, also in this case, we will rely on the following illustration:
Area of a rhombus
Look at the rhombus in the figure.
What is its area?
Given the rhombus whose length of its sides is 8 cm
The length of the given height is 5 cm
What is the area of the rhombus?
Look at the rhombus in the diagram below.
What is the area of the rhombus?
First Way
The lengths of the diagonals are multiplied and divided by .
That is:
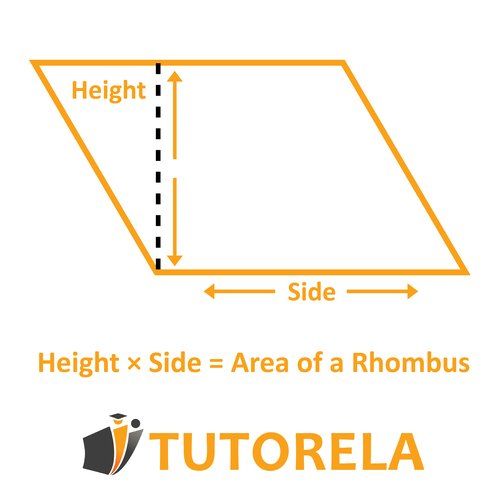
Second Way
One of the sides is multiplied by the height.
That is to say:
In the drawing given a rhombus
The length of the main diagonal 6 cm
The length of the secondary diagonal 4 cm
What is the area of the rhombus?
Calculate the area of the rhombus in the figure below:
Given the rhombus in the drawing:
What is the area?
Calculation of the Perimeter of a Rhombus
We have reached the simplest part of all, which is the calculation of the perimeter of a rhombus. Let's remember that, the perimeter of a rhombus consists of the sum of the lengths of its sides.
Because the four sides of the rhombus have the same length, knowing just one is enough. Next, we will multiply the length of one side by and obtain the perimeter of the rhombus.
Examples and Practice on the Proof of the Rhombus
Exercise No 1
Given the rhombus .
One of the angles is given. Using the data from the illustration, find the remaining three angles of the rhombus.
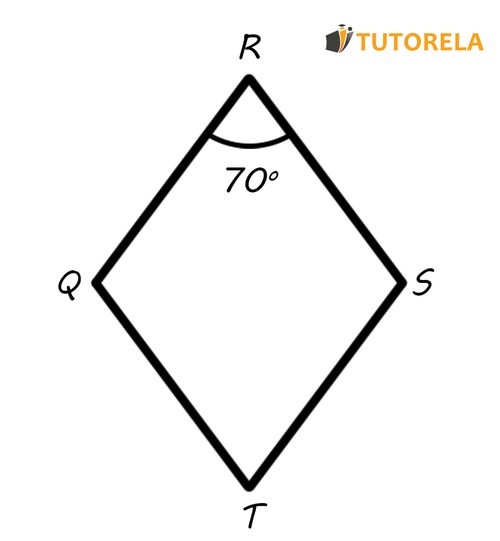
Solution:
Let's focus on the given data. We know the vertex angle which is equal to
According to what we know about the properties of the rhombus, the opposite angles have the same amplitude, therefore, the vertex angle will also be equal to .
The rhombus is a quadrilateral, therefore, the sum of all its angles is degrees, we will obtain that the sum of the angles and is: .
Let's remember again that, the opposite angles of the rhombus have the same amplitude. From this it follows that, each of the remaining vertex angles, and , will measure .
Answer: the angles of the rhombus are
Given the rhombus in the drawing:
What is the area?
Given the rhombus in the drawing:
What is the area?
A rhombus and its external height are shown in the figure below.
The length of each side of the rhombus is 5 cm.
What is its area?
Exercise No 2
Given the rhombus .
According to the data in the illustration, find the perimeter and the area of the rhombus.
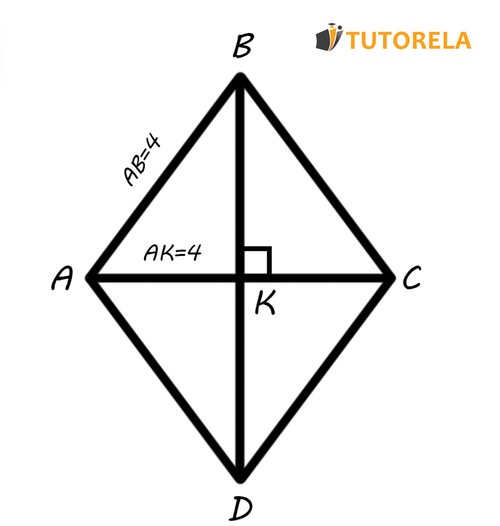
Solution:
First, we will observe the scheme. We know one of the sides of the rhombus. According to the properties we have learned, the four angles of the rhombus are equivalent.
Therefore, it follows: .
The perimeter of the rhombus is the sum of its four sides, therefore, we will multiply by and it will give us cm.
Now let's move on to calculating the area of the rhombus. To do this, we will choose the first option we studied, that is, we will multiply the diagonals and divide by .
In the illustration, it can be seen that . According to the properties of the rhombus, the intersection point of the diagonals of the rhombus crosses them, which leads to . We just need to find the second diagonal.
Let's remember another characteristic of the rhombus: the diagonals of the rhombus are perpendicular. That is, the triangle is a right triangle to which the Pythagorean theorem is applicable. Based on the Pythagorean theorem, we will calculate .
It follows:
Again, the diagonals intersect and, therefore: .
That is, it follows:
Answer:
The perimeter of the rhombus is cm.
The area of the rhombus is cm.
Examples and exercises with solutions for rhombus
Exercise #1
Look at the rhombus in the figure.
What is the relationship between the marked angles?
Step-by-Step Solution
Let's remember the different definitions of angles:
Corresponding angles are angles located on the same side of the line that intersects the two parallels and are also situated at the same level with respect to the parallel line they are adjacent to.
Therefore, according to this definition, these are the angles marked with the letter A
Alternate angles are angles located on two different sides of the line that intersects two parallels, and which are also not at the same level with respect to the parallel they are adjacent to.
Therefore, according to this definition, these are the angles marked with the letter B
Answer
A - corresponding; B - alternate
Exercise #2
Given the rhombus in the drawing:
What is the area?
Video Solution
Step-by-Step Solution
Let's remember that there are two ways to calculate the area of a rhombus:
The first is the side times the height of the side.
The second is diagonal times diagonal divided by 2.
Since we are given both diagonals, we calculate it the second way:
Answer
14
Exercise #3
Look at the rhombus in the figure.
What is its area?
Video Solution
Step-by-Step Solution
First, let's remember that according to the properties of a rhombus, all sides of a rhombus are equal,
Therefore, if we define the sides of the rhombus with the letters ABCD,
We can argue that:
AB=BC=CD=DA
We use the perimeter formula:
50 = AB+BC+CD+DA
And we can conclude that
4AB=50
(We can also use any other side, it doesn't matter in this case because they are all equal.)
We divide by four and reveal that:
AB=BC=CD=DA = 12.5
Now let's remember the formula for the area of a rhombus: the height times the side corresponding to the height.
We are given the length of the external height 8,
Now, we can replace in the formula:
8*12.5=100
Answer
100 cm²
Exercise #4
Using the rhombus in the drawing:
Calculate the area?
Video Solution
Step-by-Step Solution
Remember there are two options to calculate the area of a rhombus:
1: The diagonal multiplied by the diagonal divided by 2.
2: The base multiplied by the height.
In the question, we are only given the data for one of the diagonals and one of the sides, which means we cannot use either of the above formulas.
We need to find more data. Let's begin by finding the second diagonal:
Remember that the diagonals of a rhombus are perpendicular to one another, which means that they form a 90-degree angle.
Therefore, all the triangles in a rhombus are right-angled.
Now we can focus on the triangle where the side and the height are given, and we will calculate the third side using the Pythagorean theorem:
Insert the given data:
Now that we have found the second half of the diagonal, we can calculate the area of the rhombus by multiplying the two diagonals together.
Since the diagonals in a rhombus are perpendicular and cross each other, they are equal. Hence, our diagonals are equal:
Therefore, the area of the rhombus is:
Answer
24
Exercise #5
A rhombus has a side length measuring 7 cm.
Is DC equal to 8 cm?
Video Solution
Step-by-Step Solution
Let's recall the properties of a rhombus. In a rhombus, all sides are equal to each other, therefore DC cannot be equal to 8 cm.
Additionally, in a rhombus, there are 2 pairs of parallel and equal sides. Since the side parallel to AB is CD, it must be equal to 7 cm.
Answer
No
The rhombus in the diagram has an area of 24 cm².
What is the value of X?
Look at the rhombus in the figure.
Is it possible to calculate its area? If so, then what is it?
Look at the rhombus in the figure.
What is the relationship between the marked angles?
More Questions
Definitions, properties and Proofs
Area of a Rhombus
- Area
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Area of a trapezoid
- Perimeter of a trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Triangle Height
- The Sum of the Interior Angles of a Triangle
- Exterior angles of a triangle
- Square
- Area of a square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- Diagonals of a Rhombus
- Lines of Symmetry in a Rhombus
- From Parallelogram to Rhombus
- The Area of a Rhombus
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation
- Diagonals in a rectangle
- Symmetry in a kite









