Every geometric problem is based on data, and the solution is divided into several different questions. One of the most popular questions, and the one most likely to appear on your test, is the question about the area of a rhombus. As is well known, a rhombus consists of different triangles. If so, how do you calculate its area?
The Area of a Rhombus
How is the area of a rhombus calculated?
Rhombus Formula
- The formula to calculate the area of a rhombus: Diagonal Diagonal, divided by .
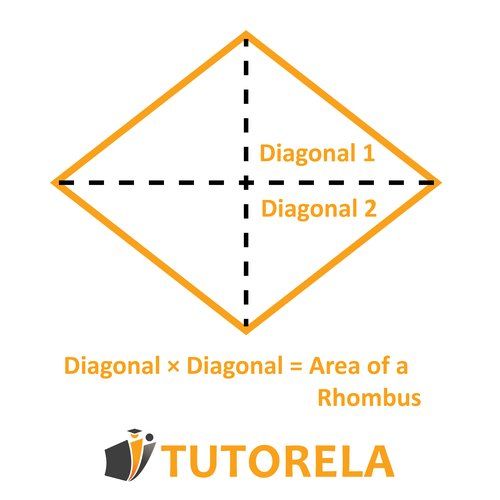
- Another formula you can think of for the area of a rhombus (depending on the information provided by the question): Base Height.
Test yourself on area of a rhombus!
Given the rhombus in the drawing:
What is the area?
The first formula to calculate the area of a rhombus.
The second formula to calculate the area of a rhombus.
Example: Calculating the Area of a Rhombus
Given the rhombus in the drawing:
What is the area?
The rhombus in the diagram has an area of 24 cm².
What is the value of X?
Given the rhombus in the drawing:
What is the area?
Rhombus Area Exercises
Below is a variety of exercises to calculate the area of a rhombus:
Example 1
- Diagonal
- Diagonal
Question:
What is the area of the rhombus?
Explanation
The calculation is done as follows: . Now, the amount should be divided by , and then the obtained answer is . So, you will calculate the area of the rhombus according to the data presented to you in the question.
Answer:
A rhombus and its external height are shown in the figure below.
The length of each side of the rhombus is 5 cm.
What is its area?
In the drawing given a rhombus
The length of each side of the rhombus is 5 cm
The length of the height of the side is 3 cm
What is the area of the rhombus?
Calculate the area of the rhombus in the figure below:
Example 2
Diagonal
Diagonal
Question:
What is the area of the rhombus?
Explanation
The area of the rhombus .
Now we divide this result by
Answer
The area of the rhombus is .
Example 3
Diagonal
Diagonal
Question:
What is the area of the rhombus?
Explanation
The area of the rhombus .
Then we divide by
Answer
The area of the rhombus is therefore .
Given the rhombus in the figure
What is your area?
Look at the rhombus in the figure.
What is its area?
Given the rhombus whose length of its sides is 8 cm
The length of the given height is 5 cm
What is the area of the rhombus?
Example 4
Calculating the area of a rhombus using the formula of base x Height:
Base
Height
Question:
What is the area of the rhombus?
Explanation
The area of the rhombus
Answer
The area of the rhombus is then .
Example 5
Calculating the area of a rhombus using the formula of base x Height:
Base
Height
Question:
What is the area of the rhombus?
Explanation
The area of the rhombus
Answer:
Look at the rhombus in the diagram below.
What is the area of the rhombus?
Given the rhombus in the figure
What is your area?
In the drawing given a rhombus
The length of the main diagonal 6 cm
The length of the secondary diagonal 4 cm
What is the area of the rhombus?
Now we will try a different exercise:
Question:
Find the value of
Explanation:
To solve the exercise, we must use the formula for the area of a rhombus, and solve it "backwards".
We will input the data we know into the formula:
We'll start by removing the denominator, multiplying the equation by .
Now, we need to isolate . To do this, we divide the equation by .
Answer
The area of the rhombus is then .
And now for a very different exercise:
Question:
What is the area of a rhombus?
Explanation:
To find the solution, we'll need to use another tool to find the missing diagonal.
We know that the diagonals of a rhombus are perpendicular to each other and divide the rhombus into four right triangles.
Therefore, we can examine our triangle and use the Pythagorean theorem to find the missing side.
We'll plug in the data we know into the Pythagorean theorem:
Now we'll construct the exercise according to the rules, to solve for .
Now we'll apply the square root to the equation to eliminate the powers
We haven't reached the solution to the exercise yet!
Now that we have found the missing side, we can use the formula for the area of a rhombus to find its area.
(Diagonal A Diagonal B): 2
It's important to remember that the data we have is not for the full diagonals, but only from the intersection point of the diagonals to the vertices.
We know that the diagonals of a rhombus also bisect each other, therefore:
Diagonal
Diagonal
Now all that's left is to plug the numbers into the formula and solve:
Answer
the area is equal to
A rhombus has an area of 40.
What is the value of X?
Given the rhombus in the figure
What is your area?
Given the rhombus in the drawing:
What is the area?
Solved Exercise: Area of a Rhombus
Solved Exercise 1 (Area of a Rhombus)
Given that the rhombus in the graphic has an area of
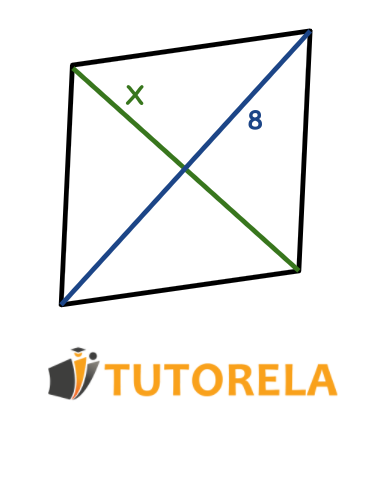
Task:
What is the value of ?
Rhombus area formula
Let's plug the data into the formula.
Now we divide by
Solved Exercise 2 (Area of a Rhombus)
Finding the diagonals from the formula:
Given the drawing of the rhombus, the area is
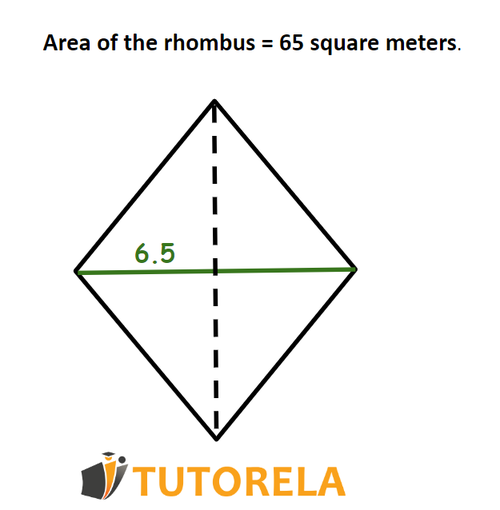
Task:
What is the length of the main diagonal in the rhombus?
Solution:
The formula for the area of a rhombus.
(Diagonal times Diagonal)/
When the area is cm²
We will denote a, which is the main and longer diagonal among the two.
we multiply both sides by
Now we divide by
Answer
The length of the main diagonal in the rhombus
Given the rhombus in the drawing:
What is the area?
The rhombus in the diagram has an area of 24 cm².
What is the value of X?
Given the rhombus in the drawing:
What is the area?
Solved Exercise 3 (Area of a Rhombus)
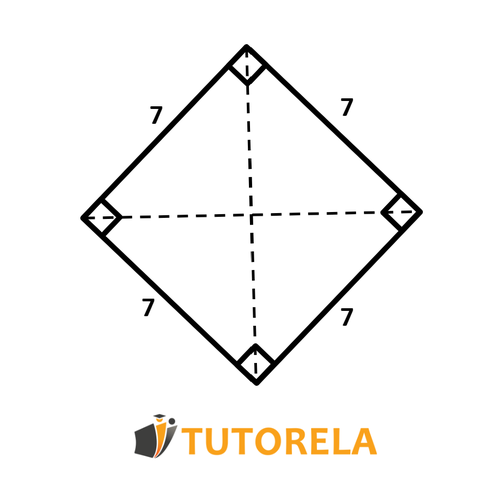
Homework:
What is the area of the rhombus?
Solution:
A rhombus whose pair of adjacent angles equals degrees is a square,
Remember that the area of a square can be calculated using the formula:
Side Side = square
We will put the numbers in the formula and solve
Answer:
The area of the rhombus or the square
Solved Exercise 4
Given the drawing of the rhombus, we have the following data as shown and
Task:
What is the area of the rhombus?
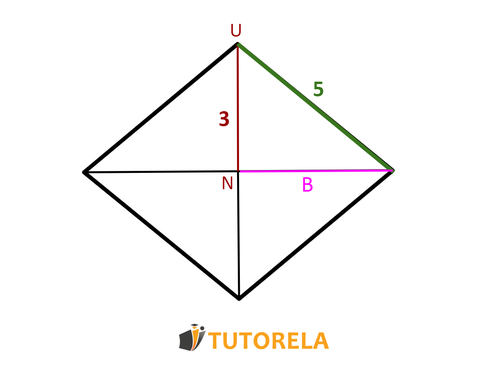
Solution:
To find the solution, we will need to use another tool to get to the missing diagonal.
We know that the diagonals of the rhombus are perpendicular to each other and divide the rhombus into four right triangles.
Therefore, we can look at our triangle and use the Pythagorean theorem to find the missing side.
We will present the data we know in the Pythagorean theorem:
Now we will move the numbers to "isolate" the .
We apply the square root to the equation to get rid of the power.
This is still not the solution to the exercise!
Now that we have found the missing side, we can use the formula for the area of a rhombus to find its area.
(Diagonal 1 Diagonal 2)
It is important to remember that the data we have is not for all the diagonals, but only from the perspective of the diagonals to the vertices.
We know that the diagonals of the rhombus also intersect each other, therefore
Diagonal 1
Diagonal 2
Now we just have to put it in the formula and solve:
Answer:
The area is equal to
A rhombus and its external height are shown in the figure below.
The length of each side of the rhombus is 5 cm.
What is its area?
In the drawing given a rhombus
The length of each side of the rhombus is 5 cm
The length of the height of the side is 3 cm
What is the area of the rhombus?
Calculate the area of the rhombus in the figure below:
Solved Exercise 5
Given the drawing of the rhombus
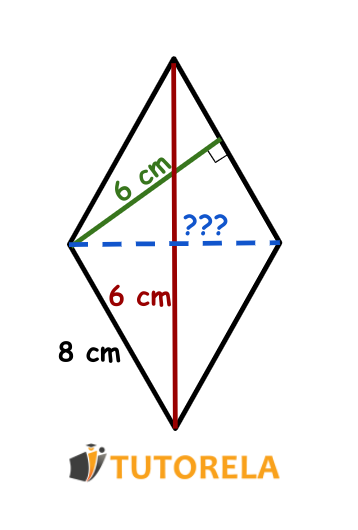
Question:
What is the length of the secondary diagonal?
Solution:
Calculate the area of the rhombus
Area of the rhombus = side X Height
It's important to remember that there is another formula to calculate the area of a rhombus
Area of the rhombus = (Diagonal 1 Diagonal 2) /
we multiply by (where and are the diagonals)
; We divide both sides by
We will introduce the area and the first diagonal into the formula and solve:
Answer:
The correct answer is cm.
Solved Exercise 6
Topic: Calculating the area of a rhombus using the ratio
Given the rhombus in the figure:
Given that the ratio between the length of the major diagonal and the minor diagonal is
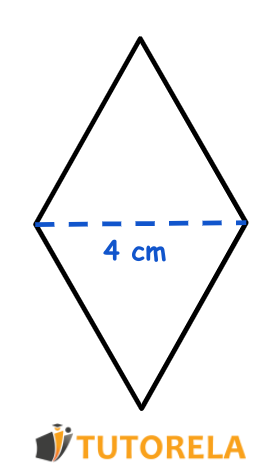
Task:
Find the area of the rhombus
Solution:
From the data that the ratio between the diagonals:
Diagonal1 / Diagonal2
In the given figure for diagonal 2 (the shorter one) we will establish its length in the formula we find.
(Multiplying diagonally)
We will divide by /
Let's calculate the area of the rhombus:
Answer:
The answer is cm²
Given the rhombus in the figure
What is your area?
Look at the rhombus in the figure.
What is its area?
Given the rhombus whose length of its sides is 8 cm
The length of the given height is 5 cm
What is the area of the rhombus?
Is there a fail proof way to score 100 on an exam?
The answer is yes and no. On one hand, they can prepare for the test in the best possible way, but still make small calculation errors (mainly due to stress), which will cause them to lose some points. In front of you, there are some tips that will significantly help your chances of getting a on a math test or exam. The key to success: perseverance!
- Attendance in math classes at school - essential! Self-study cannot replace learning the material from your teachers. If you have missed a class, make sure to catch up on the taught topic as quickly as possible.
- Doing homework consistently increases your chances of excellence. Why? Because homework allows you to practice with a variety of exercises, face challenges, and understand what your common mistakes are. Also, in the subject of math, it can be tough in training but easier in the battle (at the exam).
- Participation in class: essential! The more you participate in class, the better. Why? Because participation keeps you alert and involved in the learning process. Suggest solutions to the questions the teacher raises and ask relevant questions about the study topics.
- Private math class: welcome! No matter what your level is, your grades, and the confidence you have in yourself. Reinforcement classes strengthen your foundations, advance you both material-wise and mentally, and allow you to reap successes and higher grades.
- Plan your learning days before the test well in advance. Prepare a weekly task board, detailing learning hours and learning topics. That way, you'll always arrive ready for the exam and even be able to plan a "study-free day" the day before the exam. The goal: to arrive at the test relaxed, calm, and at peace.
Excellent Advice for Success in Math: Learn from Examples!
As is known, many times students memorize different formulas. For example: a formula to calculate the area of a rhombus. Instead of memorizing an "empty" formula without data, we memorize a formula with data. Why? Because this is an example of a question with an answer, which you can use both in preparing homework and during an exam. When you memorize an example of each topic, you have another "internal aid" that assists you and allows you to better understand additional questions.
One example of each topic is enough to "light the way" and enable you to solve questions quickly and easily. Sometimes, all you need to do is simply replace the data from the question (as indicated in the exam), when the solution is already well integrated in your mind.
Look at the rhombus in the diagram below.
What is the area of the rhombus?
Given the rhombus in the figure
What is your area?
In the drawing given a rhombus
The length of the main diagonal 6 cm
The length of the secondary diagonal 4 cm
What is the area of the rhombus?
Private Math Lesson, Also for Strengthening Formulas.
There isn't a student who isn't good at math, but there is a student who doesn't understand math. Often, what prevents students from getting good grades is not their inability, but their lack of understanding. As is known, school curriculum lessons are conducted at a certain pace, which not all students can keep up with. In this way, the gaps gradually widen and do not narrow.
Private math tutoring can strengthen the student and provide them with a quality toolbox to continue. Unlike classes in a classroom, the private lesson focuses solely on the points where the student is weak: from the difficulty of understanding what is being asked, to the difficulty of understanding how to apply the formulas based on the data presented in the question.
Private math tutoring doesn't mean you're weak!
Some students might feel a bit embarrassed to tell their peers about their intention to bridge gaps in a private math class. In practice, there's really no reason for embarrassment, quite the opposite: students who attend a private class get to reinforce the material taught in an extra session. Often, the result is that the same students who study in the private lesson are actually more advanced in the material than the rest of the class. The main advantages of the private lesson are:
- Bridging gaps: the student keeps up with the pace of the class.
- Assimilation of learned material in the form of "understanding" rather than "memorization"
- Strengthening the student's self-confidence: they prove to themselves that they can do it!
A rhombus has an area of 40.
What is the value of X?
Given the rhombus in the figure
What is your area?
Given the rhombus in the drawing:
What is the area?
How Many Private Lessons Should You Take in Math?
This is a question that does not have an unquestionable answer. Some students are interested in a private meeting once a week. However, there are students who meet with a private tutor just before tests, in order to reinforce formulas such as how to calculate the area of a rhombus, create simulations, and challenge themselves with questions that are more difficult than those expected on the test.
Given the rhombus in the drawing:
What is the area?
The rhombus in the diagram has an area of 24 cm².
What is the value of X?
Given the rhombus in the drawing:
What is the area?
Examples with solutions for Area of a Rhombus
Exercise #1
Given the rhombus in the drawing:
What is the area?
Video Solution
Step-by-Step Solution
Let's remember that there are two ways to calculate the area of a rhombus:
The first is the side times the height of the side.
The second is diagonal times diagonal divided by 2.
Since we are given both diagonals, we calculate it the second way:
Answer
14
Exercise #2
Look at the rhombus in the figure.
What is its area?
Video Solution
Step-by-Step Solution
First, let's remember that according to the properties of a rhombus, all sides of a rhombus are equal,
Therefore, if we define the sides of the rhombus with the letters ABCD,
We can argue that:
AB=BC=CD=DA
We use the perimeter formula:
50 = AB+BC+CD+DA
And we can conclude that
4AB=50
(We can also use any other side, it doesn't matter in this case because they are all equal.)
We divide by four and reveal that:
AB=BC=CD=DA = 12.5
Now let's remember the formula for the area of a rhombus: the height times the side corresponding to the height.
We are given the length of the external height 8,
Now, we can replace in the formula:
8*12.5=100
Answer
100 cm²
Exercise #3
Using the rhombus in the drawing:
Calculate the area?
Video Solution
Step-by-Step Solution
Remember there are two options to calculate the area of a rhombus:
1: The diagonal multiplied by the diagonal divided by 2.
2: The base multiplied by the height.
In the question, we are only given the data for one of the diagonals and one of the sides, which means we cannot use either of the above formulas.
We need to find more data. Let's begin by finding the second diagonal:
Remember that the diagonals of a rhombus are perpendicular to one another, which means that they form a 90-degree angle.
Therefore, all the triangles in a rhombus are right-angled.
Now we can focus on the triangle where the side and the height are given, and we will calculate the third side using the Pythagorean theorem:
Insert the given data:
Now that we have found the second half of the diagonal, we can calculate the area of the rhombus by multiplying the two diagonals together.
Since the diagonals in a rhombus are perpendicular and cross each other, they are equal. Hence, our diagonals are equal:
Therefore, the area of the rhombus is:
Answer
24
Exercise #4
Given the rhombus in the drawing:
What is the area?
Video Solution
Answer
33
Exercise #5
The rhombus in the diagram has an area of 24 cm².
What is the value of X?
Video Solution
Answer
6
- Area
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Area of a trapezoid
- Perimeter of a trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- Square
- Area of a square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- Diagonals of a Rhombus
- Lines of Symmetry in a Rhombus
- From Parallelogram to Rhombus
- The Area of a Rhombus
- Perimeter
- Areas of Polygons for 7th Grade
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- How do we calculate the area of complex shapes?
- How do we calculate the perimeter of polygons?
- Diagonals in a rectangle
- Symmetry in a kite









