Addition of Logarithms
Addition of Logarithms
Where:
is the base of the exponent
is what appears inside the log, can also appear in parentheses
is the exponent we raise the log base to in order to get the number that appears inside the log.
Adding logarithms with the same base is based on the following rule:
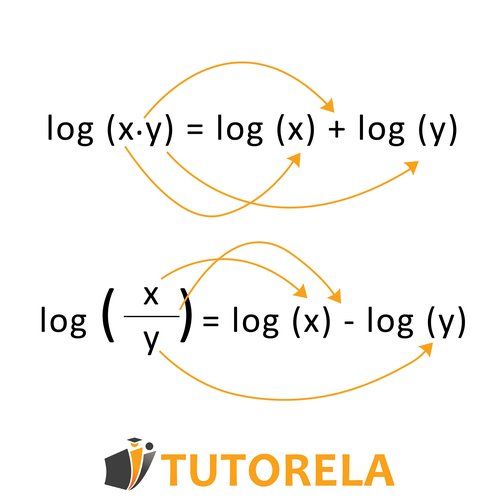
Adding logarithms with different bases is done by changing the base of the log using the following rule:

Test yourself on the sum of logarithms!
\( \log_{10}3+\log_{10}4= \)
Addition of Logarithms
Reminder - Logarithms
First, let's recall what is the definition of ?
When is the base of the log (usually )
is the exponent to which we raise
which sometimes appears in parentheses, is the number we obtain when is raised to the power of , also called the number inside the log.
In other words:
For example, if we encounter an exercise like this:
Determine which power we need to raise by in order to obtain ....?
The answer is the power of and therefore the solution is .
Addition of logarithms with the same base
In order to easily add logarithms with the same base, all you need to know is the following rule:
The rule states that if you want to add logs with the same base, you can write them as log and multiply the numbers inside the log. This will often simplify the solution process.
Let's look at an example:
If you didn't know the above, you would almost certainly encounter a problem.
To which power should we raise by in order to obtain ?... And to which power should we raise by in order to obtain ?
This is where the rule that you learned above comes in handy!
All you need to do is multiply the numbers that appear in the log whilst maintaining the same base– .
Thus we obtain the following:
As well as:
Now it's much easier for us to solve the equation!
We know that we need to raise to the power of in order to obtain and therefore the entire answer to this exercise is .
Note - This rule is valid only in cases where the base is identical. If the base was not the same in both logarithms, we could not use this rule.
Remember!
When you have the same base in both logarithms and an addition operation between them, you can multiply the numbers inside the logarithms and keep the base as it is - addition~multiplication
\( \log_24+\log_25= \)
\( \log_974+\log_9\frac{1}{2}= \)
\( 2\log_82+\log_83= \)
Addition of Logarithms with Different Bases
What happens when there is an addition exercise with logarithms of different bases?
In order to add logarithms with different bases, it's important to know the rule that allows us to change the base of a logarithm.
The goal is - to convert both logarithms to the same base.
How do you change the base of a logarithm?
Meet the logarithm change of base rule:
Now for the explanation:
When we have a logarithm with base for example and we want to convert it to another logarithm:
- Draw a fraction line.
- In the numerator, write the logarithm with the desired new base and what was in the original logarithm.
- In the denominator, write the logarithm with the desired new base and inside it put the base of the original logarithm.
Let's look at an example:
Convert the following logarithm to base :
In the numerator, we'll write log base , which is the base we want to convert to. The number inside the log in the numerator will be the original number that appears inside the log - which is .
In the denominator, we'll write again log base , the base we want to convert to, but this time, the number inside the log will be the original base - which is
Now we are able to solve the problem easily. We obtain the following:
Remember - whenever you want to convert to a different log base, you'll need to convert the log to a fraction according to the rule you just learned.
Advanced exercise: Now you can solve addition of logarithms with different bases:
We want to convert both logs to the same base and usually we'll choose the smaller base - .
Therefore:
Let's now rewrite the exercise and insert our data:
Let's insert
and obtain the following:
We obtained the solution:
\( 3\log_49+8\log_4\frac{1}{3}= \)
\( \log_47+\log_42\le\log_4x \)
\( x=\text{?} \)
\( \log_2x+\log_2\frac{x}{2}=5 \)
?=x
Examples with solutions for The Sum of Logarithms
Exercise #1
Video Solution
Step-by-Step Solution
To solve this problem, we'll apply the following steps:
- Step 1: Identify given logarithms and their base.
- Step 2: Employ the sum of logarithms property to combine the terms.
- Step 3: Calculate the resulting argument of the logarithm.
Now, let's work through each step:
Step 1: We have two logarithms: and , sharing the base of .
Step 2: Since the bases are the same, we use the sum property of logarithms:
.
Step 3: Calculate the product :
.
So, we have:
.
Therefore, the solution to the problem is .
Answer
Exercise #2
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given expression as .
- Step 2: Use the sum of logarithms rule to simplify the expression.
- Step 3: Calculate the product and express the result.
Let's work through each step:
Step 1: We have as our expression.
Step 2: Apply the sum of logarithms formula:
Step 3: Calculate the product:
Thus, .
Therefore, the solution to the problem is .
Answer
Exercise #3
Video Solution
Step-by-Step Solution
To solve this problem, we will use the property of logarithms that allows us to combine the sum of two logarithms:
- Step 1: Identify the formula. We use the property where both logarithms must have the same base.
- Step 2: Recognize the base. Here, both logarithms are in base 10: and .
- Step 3: Apply the property. Add the two logarithms using the formula: .
- Step 4: Perform the multiplication. Compute to get 12.
- Step 5: Express the result as a single logarithm: .
Therefore, the expression simplifies to .
Answer
Exercise #4
Video Solution
Step-by-Step Solution
Answer
Exercise #5
Video Solution
Step-by-Step Solution
To solve the given inequality , we will utilize the properties of logarithms:
- First, apply the logarithm sum property: .
- Now, the inequality becomes .
- Since the logarithm function is monotonically increasing when the base is greater than 1, we can simplify the inequality to .
Therefore, the solution to the inequality is .
Therefore, the correct choice is , which matches the given correct answer.
Answer
More Questions
The Sum of Logarithms
- Solve Log Equation: log7x + log(x+1) - log7 = log2x - logx
- Solve the Multi-Base Logarithm Equation: log₆₄ × log₉x = (log₆x² - log₆x)(log₉2.5 + log₉1.6)
- Solve the Logarithmic Equation: Base-8 and Base-4 Logs with Quadratic Terms
- Solve: log₂(3x) × log₅(8) = log₅(a) + log₅(2a) for Variable X
- Solve Complex Logarithmic Equation: log₅9(log₃4x + log₃(4x+1)) = 2(log₅4a³ - log₅2a)









