Logarithm Addition Practice Problems & Rules
Master adding logarithms with same and different bases. Practice problems with step-by-step solutions and change of base formula examples.
- Apply the rule log_a(x) + log_a(y) = log_a(xy) with confidence
- Convert logarithms to different bases using the change of base formula
- Solve complex addition problems with logarithms of different bases
- Simplify logarithmic expressions by combining terms correctly
- Practice real-world applications of logarithm addition properties
- Build fluency with logarithmic rules through targeted exercises
Understanding The Sum of Logarithms
Addition of Logarithms
Where:
is the base of the exponent
is what appears inside the log, can also appear in parentheses
is the exponent we raise the log base to in order to get the number that appears inside the log.
Adding logarithms with the same base is based on the following rule:
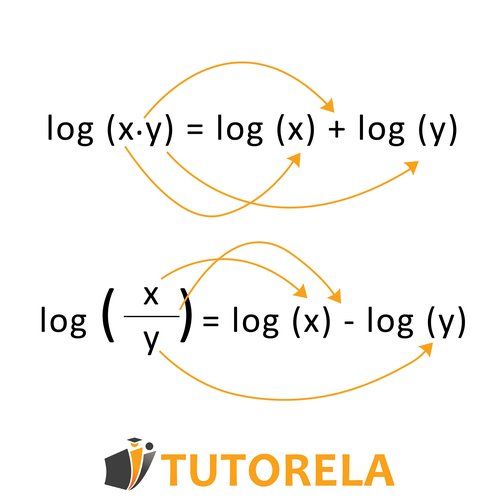
Adding logarithms with different bases is done by changing the base of the log using the following rule:

Practice The Sum of Logarithms
\( \log4x+\log2-\log9=\log_24 \)
?=x
Examples with solutions for The Sum of Logarithms
To solve this problem, we will use the property of logarithms that allows us to combine the sum of two logarithms:
- Step 1: Identify the formula. We use the property where both logarithms must have the same base.
- Step 2: Recognize the base. Here, both logarithms are in base 10: and .
- Step 3: Apply the property. Add the two logarithms using the formula: .
- Step 4: Perform the multiplication. Compute to get 12.
- Step 5: Express the result as a single logarithm: .
Therefore, the expression simplifies to .
Answer:
To solve this problem, we'll follow these steps:
- Step 1: Identify the given expression as .
- Step 2: Use the sum of logarithms rule to simplify the expression.
- Step 3: Calculate the product and express the result.
Let's work through each step:
Step 1: We have as our expression.
Step 2: Apply the sum of logarithms formula:
Step 3: Calculate the product:
Thus, .
Therefore, the solution to the problem is .
Answer:
To solve this problem, we'll apply the following steps:
- Step 1: Identify given logarithms and their base.
- Step 2: Employ the sum of logarithms property to combine the terms.
- Step 3: Calculate the resulting argument of the logarithm.
Now, let's work through each step:
Step 1: We have two logarithms: and , sharing the base of .
Step 2: Since the bases are the same, we use the sum property of logarithms:
.
Step 3: Calculate the product :
.
So, we have:
.
Therefore, the solution to the problem is .
Answer:
Answer:
Where:
y
Therefore
Answer: