Diagonals of a Rhombus

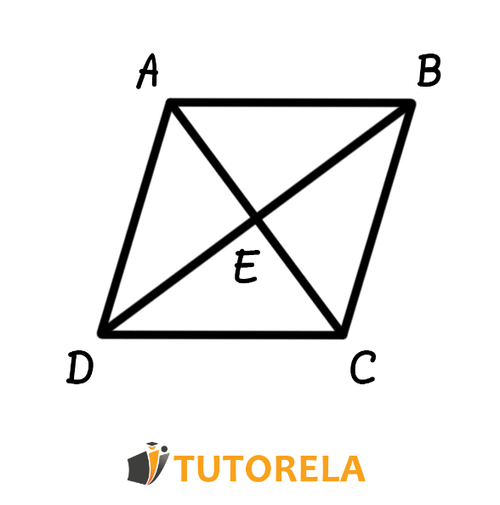
The diagonals of a rhombus have 3 properties that we can use without having to prove them:

The diagonals of a rhombus intersect. (not only do they intersect, but they do so exactly at the midpoint of each one).
The diagonals of a rhombus are perpendicular, forming a right angle of $90^o$ degrees.
The diagonals of a rhombus cross the angles of the rhombus.

The diagonals of a rhombus have 2 properties that we must prove to use them:

The diagonals of a rhombus form four congruent triangles.
The diagonals of a rhombus create equal alternate angles.

Other properties:

The lengths of the diagonals of a rhombus are not equal.

The product of the diagonals divided by 2 is equal to the area of the rhombus:
$\frac{product~of~the~diagonals}{2}=area~of~rhombus$

Practice Diagonals of a Rhombus

Question 1

Do the diagonals of the rhombus above intersect each other?

Question 2

Look at the following rhombus:

Are the diagonals of the rhombus parallel?

Question 3

Look at the following rhombus:

Are the diagonals of the rhombus perpendicular to each other?

Question 4

Given the rhombus:

How much is it worth? $$ ∢A $$ ?

Question 5

Look at the following rhombus:

Can a rhombus have diagonals that are equal?

Examples with solutions for Diagonals of a Rhombus

Exercise #1

Do the diagonals of the rhombus above intersect each other?

Step-by-Step Solution

In a rhombus, all sides are equal, and therefore it is a type of parallelogram. It follows that its diagonals indeed intersect each other (this is one of the properties of a parallelogram).

Therefore, the correct answer is answer A.

Answer

Yes

Exercise #2

Look at the following rhombus:

Are the diagonals of the rhombus parallel?

Step-by-Step Solution

The diagonals of the rhombus intersect at their point of intersection, and therefore are not parallel

Answer

No.

Exercise #3

Look at the following rhombus:

Are the diagonals of the rhombus perpendicular to each other?

Step-by-Step Solution

The diagonals of the rhombus are indeed perpendicular to each other (property of a rhombus)

Therefore, the correct answer is answer A.

Answer

Yes.

Exercise #4

Given the rhombus:

How much is it worth? $∢A$ ?

Video Solution

Step-by-Step Solution

The rhombus is a type of parallelogram, therefore its opposite angles are equal (property of parallelograms), so:

$∢A =50\degree$ Therefore, the correct answer is answer A.

Answer

Exercise #5

Look at the following rhombus:

Can a rhombus have diagonals that are equal?

Video Solution

Answer

Yes.

Question 1

Given the rhombus:

How much is it worth? $$ ∢D $$ ?

Question 2

Given the rhombus:

How much is it worth? $$ ∢B $$ ?

Question 3

Given the rhombus:

How much is it worth? $$ ∢A $$ ?

Question 4

Given the rhombus:

Is every rhombus a square?

Question 5

Given the rhombus:

Is every square a rhombus?

Exercise #6

Given the rhombus:

How much is it worth? $∢D$ ?

Video Solution

Answer

Exercise #7

Given the rhombus:

How much is it worth? $∢B$ ?

Video Solution

Answer

130

Exercise #8

Given the rhombus:

How much is it worth? $∢A$ ?

Video Solution

Answer

Exercise #9

Given the rhombus:

Is every rhombus a square?

Video Solution

Answer

Not true

Exercise #10

Given the rhombus:

Is every square a rhombus?

Video Solution

Answer

True

Question 1

Given the rhombus:

How much is it worth? $$ ∢B $$ ?

Question 2

Given the rhombus:

How much is it worth? $$ ∢D $$ ?

Question 3

Given the rhombus:

How much is it worth? $$ ∢C $$ ?

Question 4

Given the rhombus:

How much is it worth? $$ ∢A $$ ?

Question 5

Given the rhombus:

How much is it worth? $$ ∢B $$ ?

Exercise #11

Given the rhombus:

How much is it worth? $∢B$ ?

Video Solution

Answer

140

Exercise #12

Given the rhombus:

How much is it worth? $∢D$ ?

Video Solution

Answer

Exercise #13

Given the rhombus:

How much is it worth? $∢C$ ?

Video Solution

Answer

150

Exercise #14

Given the rhombus:

How much is it worth? $∢A$ ?

Video Solution

Answer

Exercise #15

Given the rhombus:

How much is it worth? $∢B$ ?

Video Solution

Answer

130

Topics learned in later sections

Diagonals of a Rhombus - Examples, Exercises and Solutions