Perpendicular lines are vertical lines that form a right angle between them, that is, an angle of degrees.
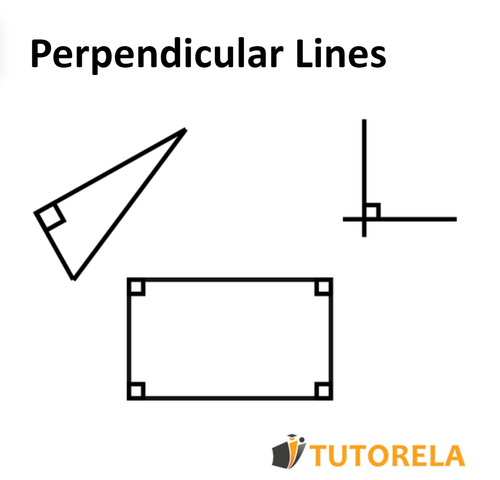
Perpendicular lines appear in many geometric shapes, such as a rectangle, a square, a right triangle, and others.
Perpendicular Lines
Test yourself on perpendicular lines!
Determine which lines are parallel to one another?
Some examples of perpendicular lines
Perpendicular lines that form a degree angle between them.
Perpendicular lines in a right triangle.
Perpendicular lines in a rectangle: the adjacent sides in the rectangle are perpendicular to each other.
Examples and exercises with solutions of perpendicular lines
Exercise #1
Determine which lines are parallel to one another?
Video Solution
Step-by-Step Solution
Remember that parallel lines are lines that, if extended, will never intersect.
In diagrams a'+b'+c', all the lines intersect with each other at a certain point, except for diagram d'.
The lines drawn in answer d' will never intersect.
Answer
Exercise #2
Which lines are perpendicular to each other?
Video Solution
Step-by-Step Solution
Let's remember that perpendicular lines are lines that form a right angle of 90 degrees between them.
The only drawing where it can be seen that the lines form a right angle of 90 degrees between them is drawing A.
Answer
Exercise #3
Which lines are perpendicular to each other?
Video Solution
Step-by-Step Solution
Perpendicular lines are lines that form a right angle of 90 degrees between them.
The only drawing where the lines form a right angle of 90 degrees between them is drawing A.
Answer
Exercise #4
Which figure(s) show intersecting lines?
Video Solution
Step-by-Step Solution
Lines that intersect each other are lines that meet or cross each other.
The diagrams showing lines that cross each other are 1 and 3.
In diagram 2, the lines are perpendicular and vertical to each other, while in drawing 4, the lines are parallel to each other.
Answer
1 and 3
Exercise #5
Which figure shows perpendicular lines?
Video Solution
Step-by-Step Solution
Perpendicular lines are lines that form a right angle between them.
In the drawings A+C+D, you can see that the angles formed are not right angles.
It is possible to point out a right angle in drawing B.
Answer
Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1
Which lines are perpendicular to each other?
Question 2
Which lines are perpendicular to each other?
Question 3
Which figure(s) show intersecting lines?
More Questions
Perpendicular Lines
- Counting Perpendicular Lines: Finding All Line Pairs in a Square
- Counting Perpendicular Lines: Analysis of Nested Square Geometry
- Finding Perpendicular Line Pairs: Cross-Shaped Geometric Analysis
- Counting Perpendicular Lines: Identifying Right Angle Pairs in a Geometric Diagram
- Counting Perpendicular Lines: Geometric Diagram Analysis Exercise
Related Subjects
- Area
- Trapezoids
- Area of a trapezoid
- Perimeter of a trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Parallel lines
- Proving Parallel Lines
- Angles In Parallel Lines
- Alternate angles
- Corresponding angles
- Collateral angles
- Vertically Opposite Angles
- Adjacent angles
- Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- Perimeter
