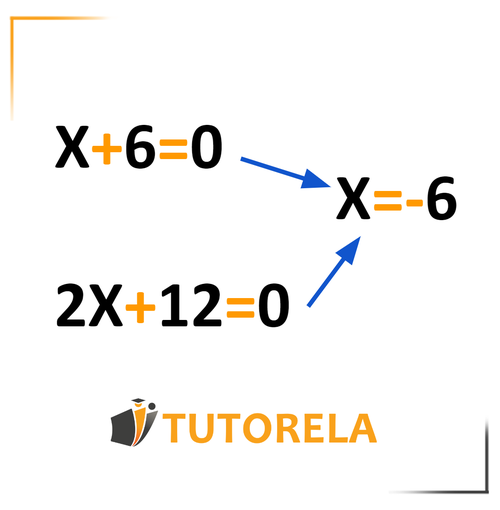
Equivalent Equations
Equivalent equations are different equations whose basically equal to each other, as they share the same variable, in addition to sharing the same solution. That means that if two equations simplify to the same solution when solved, they are equivalent.
We can easily move from one equivalent equation to another. In fact, each equation has an infinity of equivalent equations. This is due to the following: if you add, subtract, multiply, or divide both sides of an equation by a number different from zero, another equation equivalent to the initial one is obtained.
The importance of equivalent equations
By using equivalent equations, we can basically change the equation step by step, without changing it solution. In other words, using equivalent equations to maintain equality, helps us simplify complex expressions or isolate variables.