In fact, estimation allows us to guess (hence the redundancy) the supposed result, without performing the exact calculation.
That is, in certain cases, we don't need to know the solution precisely, a rough idea is sufficient to solve a particular mathematical problem.
Sometimes we are asked to compare mathematical expressions, draw deductions from one exercise to another, round numbers to simplify a calculation, and other similar tasks.
For example:
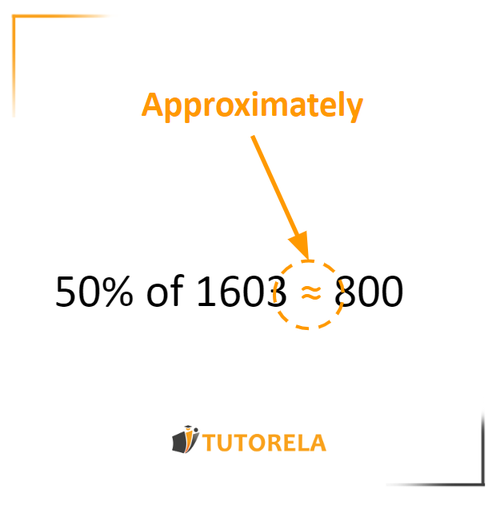
It can be estimated that half of 1603 is approximately 800.