Volume of Orthohedron Practice Problems & Solutions

To solve this problem, we'll follow these steps:

• Identify the given dimensions of the rectangular prism.
• Use the formula for volume: $V = l \times w \times h$.
• Calculate the volume by plugging in the given values.

Now, let's work through each step:
Step 1: The problem provides the dimensions of the prism: length = 3, width = 8, height = 2.
Step 2: Applying the formula, we have $V = l \times w \times h = 3 \times 8 \times 2$.
Step 3: Performing the multiplication, we obtain $V = 3 \times 8 \times 2 = 24 \times 2 = 48$.

Therefore, the volume of the rectangular prism is $48$.

To solve this problem, we'll follow these steps:

• Step 1: Identify the given dimensions of the prism.
• Step 2: Apply the formula for the volume of a rectangular prism.
• Step 3: Perform the necessary calculations.

Now, let's work through each step:
Step 1: The given dimensions are height $h = 5$, width $w = 4$, and depth $d = 9$.
Step 2: We use the formula for volume $V = h \times w \times d$.
Step 3: Plugging in our values, we have
$V = 5 \times 4 \times 9 = 180$

Therefore, the volume of the rectangular prism is $180$.

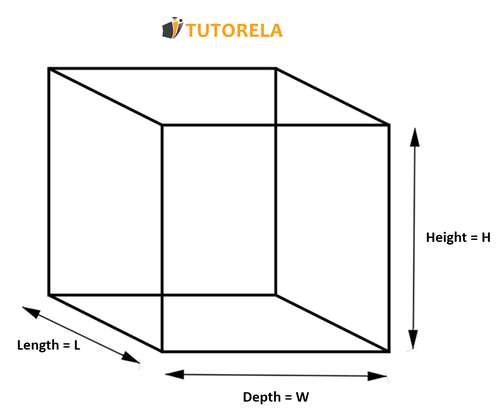
To solve this problem, we need to find the volume of the rectangular prism by following these steps:

• Step 1: Identify the given dimensions.
• Step 2: Apply the formula for the volume of a rectangular prism.
• Step 3: Plug in the values and calculate the volume.

Let's proceed with each step:

Step 1: We are given the length = 5 units, width = 8 units, and height = 12 units of the prism.

Step 2: Use the formula for the volume of a rectangular prism:
$\text{Volume} = \text{length} \times \text{width} \times \text{height}$

Step 3: Substitute the given dimensions into the formula:
$\text{Volume} = 5 \times 8 \times 12$

Now, perform the calculation:
$5 \times 8 = 40$
$40 \times 12 = 480$

Thus, the volume of the rectangular prism is $480$ cubic units.

Therefore, the correct choice from the given options, based on this calculation, is Choice 3: $480$.

To solve this problem, we need to identify the correct formula for the volume of a cuboid:

A cuboid is defined by three dimensions: length ($l$), width ($w$), and height ($h$). To find the volume of a cuboid, we use the formula:

$V = l \times w \times h$

Given the answer choices:

• Choice 1: $l \times 2 \times w$
• Choice 2: $l \times w \times h$
• Choice 3: $l \times w$
• Choice 4: $w \times h$

The formula for the volume of a cuboid is explicitly listed in Choice 2, which is $l \times w \times h$. This matches the standard mathematical formula for volume.

Thus, the correct answer to the problem is Choice 2: $\text{length } \times \text{width } \times \text{height}$.

The formula to calculate the volume of a cuboid is:

height*length*width

We replace the data in the formula:

3*5*7

7*5 = 35

35*3 = 105