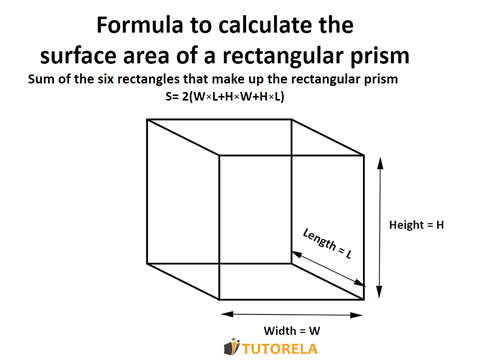
Rectangular Prisms are made up of different rectangles. When faced with an exercise or exam that asks you to calculate the surface area of a rectangular Prism, use the formula below.
Surface Area of a Cuboid Practice Problems & Solutions
Master surface area of cuboid calculations with step-by-step practice problems. Learn formulas, solve real-world applications, and boost your geometry skills today.
- Apply the surface area formula SA = 2(lw + lh + wh) to rectangular prisms
- Calculate surface area using length, width, and height measurements accurately
- Solve real-world problems involving boxes, containers, and packaging materials
- Convert between different units of measurement in surface area calculations
- Identify and correct common mistakes in cuboid surface area problems
- Build confidence with progressively challenging surface area word problems
Understanding Surface Area of a Cuboid
The formula: how to calculate the area of a rectangular prism (rectangular orthohedron)?
S= surface area
Practice Surface Area of a Cuboid
A cuboid has a surface area of 102.
Calculate X.
Examples with solutions for Surface Area of a Cuboid
A cuboid is shown below:
What is the surface area of the cuboid?
Remember that the formula for the surface area of a cuboid is:
(length X width + length X height + width X height) 2
We input the known data into the formula:
2*(3*2+2*5+3*5)
2*(6+10+15)
2*31 = 62
Answer:
62
Look at the cuboid below.
What is its surface area?
We identified that the faces are
3*3, 3*11, 11*3
As the opposite faces of an cuboid are equal, we know that for each face we find there is another face, therefore:
3*3, 3*11, 11*3
or
(3*3, 3*11, 11*3 ) *2
To find the surface area, we will have to add up all these areas, therefore:
(3*3+3*11+11*3 )*2
And this is actually the formula for the surface area!
We calculate:
(9+33+33)*2
(75)*2
150
Answer:
150
Look at the cuboid below.
What is the surface area of the cuboid?
Let's see what rectangles we have:
8*5
8*12
5*12
Let's review the formula for the surface area of a rectangular prism:
(length X width + length X height + width X height) * 2
Now let's substitute all this into the exercise:
(8*5+12*8+12*5)*2=
(40+96+60)*2=
196*2= 392
This is the solution!
Answer:
392 cm²
What is the surface area of the cuboid in the figure?
To solve this problem, we'll follow these steps:
- Step 1: Identify the dimensions of the cuboid.
- Step 2: Apply the surface area formula for a cuboid.
- Step 3: Calculate and interpret the result.
Now, let’s work through each step:
Step 1: We have the dimensions as follows:
- Length () = 72
- Width () = 17
- Height () = 14
Step 2: Apply the surface area formula:
The total surface area is calculated using the formula:
Substitute the given dimensions into the formula:
Step 3: Calculate each multiplication and sum them up:
- Calculate
- Calculate
- Calculate
Now substitute back into the equation:
Add the products:
Finally, multiply by 2:
Therefore, the surface area of the cuboid is .
Answer:
4940
Calculate the surface area of the orthohedron below using the data in the diagram.
To solve this problem, we'll utilize the formula for the surface area of a cuboid. The steps are as follows:
- Step 1: Identify the dimensions from the problem. The dimensions provided are , , and .
- Step 2: Apply the surface area formula for a cuboid. The formula is: where , , and are the dimensions of the cuboid.
- Step 3: Substitute the known values into the formula:
- Step 4: Calculate each term inside the parentheses: - - -
- Step 5: Sum the results from Step 4:
- Step 6: Multiply the sum by 2 to find the total surface area:
Thus, after performing the necessary calculations, the surface area of the orthohedron is square units.
Answer:
62