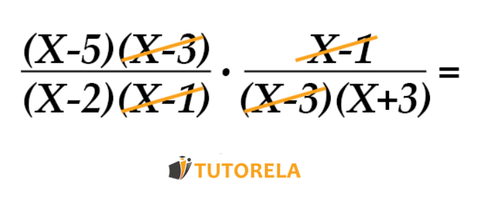Identify the field of application of the following fraction:
−2+x8
Let's examine the following expression:
−2+x8
As we know, the only restriction that applies to division is division by 0, given that no number can be divided into 0 parts. Hence division by 0 is undefined.
Therefore, when we talk about a fraction, where the dividend (the number being divided) is in the numerator, and the divisor (the number we divide by) is in the denominator, the restriction applies only to the denominator, which must be different from 0,
In the given expression:
−2+x8
As stated, the restriction applies to the fraction's denominator only,
Therefore, in order for the given expression (the fraction - in this case) to be defined, we require that the expression in its denominator - does not equal zero, in other words:
−2+x=0
We will solve this inequality, which is a point inequality of first degree, in the same way we solve a first-degree equation, meaning - we isolate the variable on one side, by moving terms (and dividing both sides of the inequality by its coefficient if needed):
−2+x=0x=2
Therefore, the domain (definition domain) of the given expression is:
x=2
(This means that if we substitute any number different from 2 for x, the expression will remain well-defined),
Therefore, the correct answer is answer C.
Note:
In a general form - solving an inequality of this form, meaning, a non-graphical, but point inequality - that uses the = sign and not the inequality signs: ,>,<,≥,≤, is identical in every way to an equation and therefore is solved in the same way and all rules used to solve an equation of any type are identical for it as well.