Numerator

What is the numerator? The numerator is the top number of a fraction and represents the portion within the whole part.

For example:

Detailed explanation

Start practice

Test yourself on simple fractions!

Without calculating, determine whether the quotient in the division exercise is less than 1 or not:

$$ 5:6= $$

Practice more now

Numerator

In this article, you will learn everything you need to know about the numerator and its function in fractions.

What is the numerator?

The numerator is one of the components of the fraction, therefore, to better understand what the numerator is, let's first talk about fractions.
A fraction is a number that is composed of two numbers:
The top one which is called the numerator
A fraction bar that represents division
And the bottom number which we call denominator

For example:

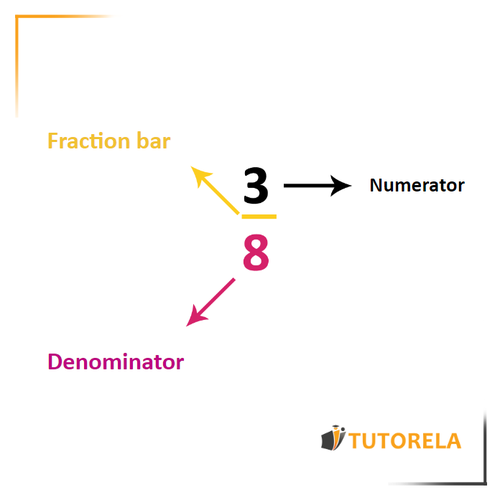
A2 - A fraction is a number that is made up of two numbers

The fraction could represent a certain part or even the entirety of a whole number.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Without calculating, determine whether the quotient in the division exercise is less than 1:

$$ 7:11 $$

Question 2

Without calculating, determine whether the quotient in the following division is less than 1:

$$ 11:8 $$

Question 3

Without calculating, determine whether the quotient in the division exercise is smaller than 1 or not:

$$ 2:1 $$

What function does the numerator serve?

The numerator represents a certain part within the whole.
For example, in the fraction
$5\over 8$ ,
The numerator 5 represents 5 eighths –> $5$ portions or parts within $8$ .
Explanatory note as a gift: The $8$ in the denominator represents the whole –> $8$
parts or portions

Let's see it illustrated:

The denominator 8 represents the division into 8 parts

Now that you know everything you need about the numerator, let's practice!
Discover the fractions with numerator $1$ :
$\frac{1}{3}, \frac{5}{1}, \frac{1}{1}, \frac{5}{5},$

Solution:
$\frac{1}{3}$
In this fraction, the numerator is $1$ –> the number located at the top.

$\frac{1}{1}$
In this fraction, the numerator is $1$ –> the number located at the top.

Write $3$ fractions that have the number $2$ in the numerator

Solution:
$\frac{2}{2}, \frac{2}{4}, \frac{2}{3},$

In the three fractions we wrote, the numerator is $2$ . Any fraction you write with $2$ in the numerator and with any whole number except $0$ in the denominator, will be a correct answer.

Examples and exercises with solutions of Numerator

Exercise #1

Without calculating, determine whether the quotient in the division exercise is less than 1 or not:

$5:6=$

Video Solution

Step-by-Step Solution

Note that the numerator is smaller than the denominator:

$5 < 6$

As a result, we can write it thusly:

$\frac{5}{6} < 1$

Therefore, the quotient in the division exercise is indeed less than 1.

Answer

Less than 1

Exercise #2

Without calculating, determine whether the quotient in the division exercise is less than 1:

$7:11$

Video Solution

Step-by-Step Solution

Note that the numerator is smaller than the denominator:

$7 < 11$

As a result, we can write it thusly:

$\frac{7}{11}<1$

Therefore, the quotient in the division exercise is indeed less than 1.

Answer

Less than 1

Exercise #3

Without calculating, determine whether the quotient in the following division is less than 1:

$11:8$

Video Solution

Step-by-Step Solution

Note that the numerator is smaller than the denominator:

$11 > 8$

As a result, it can be written like this:

$\frac{11}{8} > 1$

Therefore, the quotient in the division problem is not less than 1.

Answer

Not less than 1

Exercise #4

Without calculating, determine whether the quotient in the division exercise is smaller than 1 or not:

$2:1$

Video Solution

Step-by-Step Solution

We know that every fraction 1 equals the number itself.

We also know that 2 is greater than 1.

Similarly, if we convert the expression to a fraction:

2/1

We can see that the numerator is greater than the denominator. As long as the numerator is greater than the denominator, the number is greater than 1.

Answer

Exercise #5

Without calculating, determine whether the quotient in the division exercise is less than 1 or not:

$1:2=$

Video Solution

Step-by-Step Solution

Note that the numerator is smaller than the denominator:

$1 < 2$

As a result, we can claim that:

$\frac{1}{2}<1$

Therefore, the fraction in the division problem is indeed less than 1.

Answer

Yes

Do you know what the answer is?

Question 1

Without calculating, determine whether the quotient in the division exercise is less than 1 or not:

$$ 1:2= $$

Question 2

My numerator is 8 and my denominator is 11.

Which fraction am I?

Question 3

My numerator is 3 and my denominator is 8.

Which fraction am I?

Start practice