Denominator

In this article, you will learn everything you need to know about the denominator and its function in fractions.

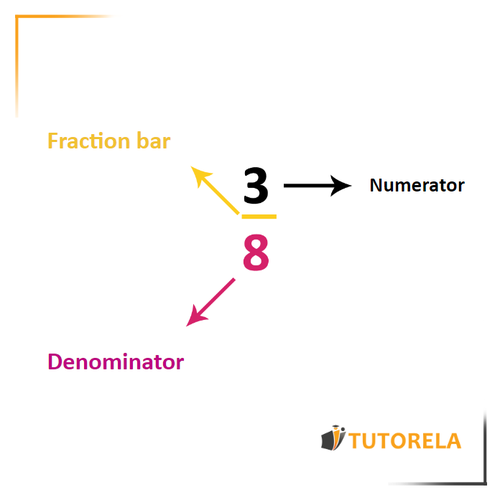
The denominator is one of the components of a fraction, therefore, to better understand what the denominator is, let's first talk about fractions.
A fraction is a number that is composed of two numbers:
The upper one which is called the numerator
A fractional line that represents a division
And the lower number which we call the denominator

For example:

The fraction could represent a certain part or even the entirety of a whole.

The denominator represents the whole itself, that is, the totality of parts or portions there are.
For example, in the fraction
 $7 \over 8$,
The denominator indicates that $8$ is the whole, in total there are $8$ parts.
Explanatory note as a gift: The $7$ in the numerator represents a certain part within the whole $7$ parts within $8$, that is, $7$ eighths.

Let's see it illustrated:

Discover the fractions whose denominator is $2$:
$\frac{2}{3}, \frac{5}{2}, \frac{2}{2}, \frac{7}{7}$

Solution:
$\frac{5}{2}$
In this fraction, the denominator is $2$ –> the number located at the bottom.

$\frac{2}{2}$
In this fraction, the denominator is $2$ –> the number located at the bottom.

Write $3$ fractions whose denominator is $5$:

Solution:
$\frac{2}{5}, \frac{12}{5}, \frac{5}{5}$

In the three fractions we wrote, the denominator is $5$. Any fraction you write that has the number $5$ as the denominator and any whole number as the numerator will be a correct answer.