What are Percentages?
In order to recognise and calculate percentages, we need to understand two basic concepts:
Master percentage calculations with step-by-step practice problems. Learn to find parts of a whole, calculate discounts, and solve real-world percentage word problems.
In order to recognise and calculate percentages, we need to understand two basic concepts:
When we are discussing percentages, one should always ask the question "percentage of what?", meaning, there must be some whole from which the percentage is calculated. The whole serves as a reference point for the percentages.
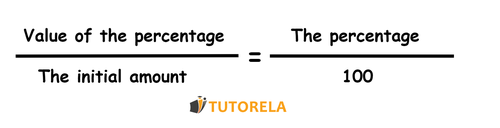
Calculate 8% of 100:
Calculate 30 over 100 as a percentage:
In order to determine what percentage 30 is out of 100, you can use the following formula:
We begin by substituting the given values into the formula:
We then proceed to simplify the expression:
Therefore, 30 out of 100 is 30%.
Answer:
30%
Calculate 3% of 100:
To solve this problem, we'll proceed with the following steps:
Therefore, the 3% of 100 is .
Answer:
3
Calculate 32 over 100 as a percentage:
To solve this problem, we'll follow these steps:
Now, let's work through each step:
Step 1: The problem gives us the fraction .
Step 2: Since the denominator is 100, the fraction directly represents a percentage.
Step 3: This means that is simply .
Therefore, the solution to the problem is .
Answer:
32%
Calculate 25 over 100 as a percentage:
In order to determine what percentage 25 is out of 100, we use the following formula:
.
We begin by substituting in the known values:
.
Thus, 25 out of 100 is .
Answer:
25%
Calculate 40 over 100 as a percentage:
In order to determine what percentage 40 is out of 100, we use the following formula:
We begin by substituting in the known values:
We then proceed to solve the expression:
Thus, 40 out of 100 is 40%.
Answer:
40%