Percentage Problems Practice - Calculate Discounts & Values

Master percentage calculations with step-by-step practice problems. Learn to find percentages, calculate discounts, and solve real-world percentage word problems.

📚Master Percentage Calculations with Interactive Practice
  • Calculate percentages using the fundamental formula: percentage value/initial amount = percentage/100
  • Solve discount problems to find sale prices and savings amounts
  • Find what percentage one number is of another using cross multiplication
  • Work with percentage increases and decreases in real-world scenarios
  • Convert between fractions, decimals, and percentages with confidence
  • Apply percentage formulas to word problems involving money, quantities, and measurements

Understanding Percentage

Complete explanation with examples

Formula to calculate a percentage

What is a percentage?

A percentage is a way to define a part, or fraction of a total.

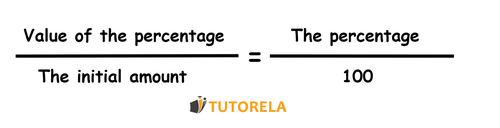
When we discuss percentages, we should ask ourselves the following: "the percentage of what?". Saying 50% without specifying the whole, fails to make sense. Instead one should say " 50% 50\% of 80 80 " is 40 40 . In summary, the percentage represents what part of 100 100 is the number in question.

The percentage symbol is % \% :
When we want to express that a%a\%
We should write it as follows: a100a \over 100

In order to solve percentage problems, we apply the following formula

Percentage valueInitial amount=The percentage100 \frac{Percentage~value}{Initial~amount}=\frac{The~percentage}{100}

Percentage value: is the actual value that this percentage represents.

Initial amount: is the initial figure before being changed.
Percentage: is the percentage of change.

To solve percentage problems, we will use the following formula

You can apply this formula to any percentage exercise, as long as you note the data correctly, and verify what has been asked.

Detailed explanation

Practice Percentage

Test your knowledge with 26 quizzes

Calculate 25 over 100 as a percentage:

Examples with solutions for Percentage

Step-by-step solutions included
Exercise #1

Calculate 15% of 100:

Step-by-Step Solution

To find 15% of 100, you can convert the percentage to a decimal by dividing by 100:

15%=15100=0.15 15\% = \frac{15}{100} = 0.15

Next, multiply this decimal by 100:

0.15×100=15 0.15 \times 100 = 15

Thus, 15% of 100 is 15.

Answer:

15 15

Exercise #2

Calculate 35% of 100:

Step-by-Step Solution

To find 35% of 100, first convert the percentage into a decimal by dividing by 100: 35%=35100=0.35 35\% = \frac{35}{100} = 0.35 .

Then, multiply this decimal by 100: 0.35×100=35 0.35 \times 100 = 35 .

Therefore, 35% of 100 is 35 35 .

Answer:

35 35

Exercise #3

Calculate 3% of 100:

Step-by-Step Solution

To solve this problem, we'll proceed with the following steps:

  • Step 1: Identify the given information
    We are given a percentage of 3% and a whole number of 100.
  • Step 2: Use the percentage formula
    The formula to calculate the percentage of a whole number is given by:
    Percentage value=percentage100×whole number \text{Percentage value} = \frac{\text{percentage}}{100} \times \text{whole number}
  • Step 3: Substitute the values and calculate
    Substituting the given values into the formula, we have:
    3100×100=3 \frac{3}{100} \times 100 = 3

Therefore, the 3% of 100 is 3 3 .

Answer:

3

Video Solution
Exercise #4

Calculate 45% of 100:

Step-by-Step Solution

To find 45% of 100, you can multiply the percentage as a decimal by the whole number. First, convert 45% into a decimal. This is done by dividing by 100: 45%=45100=0.45 45\% = \frac{45}{100} = 0.45 .

Then, multiply this decimal by 100: 0.45×100=45 0.45 \times 100 = 45 .

Therefore, 45% of 100 is 45 45 .

Answer:

45 45

Exercise #5

Calculate 50% of 100:

Step-by-Step Solution

In order to determine 50% of 100, we first convert the percentage into a decimal. Convert 50% to a decimal: 50%=0.5 50\% = 0.5 .

Next, multiply the decimal by 100 to get the percentage value: 0.5×100=50 0.5 \times 100 = 50 .

Therefore, 50% of 100 is 50 50 .

Answer:

50 50

Frequently Asked Questions

Everything you need to know about Percentage

What is the basic formula for calculating percentages?

+
The fundamental percentage formula is: (Percentage value / Initial amount) = (The percentage / 100). This can be rearranged to solve for any missing value. For example, to find 30% of 120, you would calculate: X/120 = 30/100, then cross multiply to get X = 36.

How do I calculate a discount percentage on a sale price?

+
To find a discount: 1) Multiply the percentage by the original price, 2) Divide by 100 to get the discount amount, 3) Subtract from original price. For example, a 25% discount on $200: (25 × 200) ÷ 100 = $50 discount, so final price is $200 - $50 = $150.

What's the difference between finding a percentage OF something versus finding what percentage something IS?

+
Finding a percentage OF uses: (percentage/100) × total = result. Finding what percentage something IS uses: (part/whole) × 100 = percentage. For example: 20% of 50 = 10, but 10 is 20% of 50.

How do I solve percentage word problems step by step?

+
Follow these steps: 1) Identify what represents 100% (the whole), 2) Identify the percentage given, 3) Determine what you're solving for, 4) Set up the proportion using the formula, 5) Cross multiply and solve. Always ask yourself 'percentage of what?' to identify the whole.

Why do I get a number higher than the original when calculating percentage increases?

+
When something increases by a percentage, the result represents more than 100% of the original. For example, if a $50 item increases to $58, it's now at 116% of its original price (a 16% increase). Values above 100% indicate growth beyond the starting amount.

How do I convert fractions to percentages quickly?

+
Multiply the fraction by 100. For example: 3/5 × 100 = 300/5 = 60%. This works because percent means 'per hundred,' so you're finding how many parts per 100 the fraction represents.

What's the trick for calculating 10%, 25%, and 50% mentally?

+
Use these shortcuts: 10% = divide by 10, 25% = divide by 4, 50% = divide by 2. For other percentages, combine these: 30% = 10% × 3, 75% = 25% × 3. For example: 25% of 80 = 80 ÷ 4 = 20.

How do I check if my percentage calculation is correct?

+
Use reverse calculation: if 30% of 120 = 36, then 36/120 × 100 should equal 30%. Also, sense-check your answer: 50% should be half, 25% should be one-quarter, 10% should be one-tenth of your starting number.

More Percentage Questions

Click on any question to see the complete solution with step-by-step explanations

Quantity, percentage, percentage value

Calculate 25% of 160: Percentage Equation Breakdown Calculate 12% of 25: Step-by-Step Percentage Solution Find the Total Students: Solving the 1/5 and 20% Participation Problem Calculate 25% of 124 Tables: Finding Chinese Manufacturing Count Solve for Total: Finding Shop Inventory When 30% = Standard Issue Dolls

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Applying the formula Calculate the percentage of the whole number Calculation using percentages Change in two elements Convert fractions to percentages Express one number as a percentage of another Finding the whole using a part Pricing strategies including discounts and markups The Whole number is 100 The Whole number is a Multiple of 100 The Whole number is Greater than 100 Two changes in percentages Worded problems

More Resources and Links

Explore more resources and links related to Percentage
Practice EstimationPractice PercentagesPractice How do you calculate the percentage value?Practice What is a percentage?Practice Converting between fractions and percentages and vice versa