A percentage is a number that expresses a part of .
Quantity refers to the absolute number of something.
The percentage value refers to the quantity that corresponds to the specific percentage of the whole.
Percentage Practice Problems & Word Problems with Solutions
Master percentage calculations with step-by-step practice problems. Learn to find percentage values, convert percentages to numbers, and solve real-world applications.
- Calculate percentage values using the fundamental percentage formula
- Convert percentages to actual numbers in real-world scenarios
- Find what percentage one number is of another
- Determine total quantities when given percentage and percentage value
- Solve discount and price reduction percentage problems
- Apply percentage concepts to classroom and everyday situations
Understanding Percentage
What is a percentage?
In order to solve questions about finding the quantity, percentage and percentage value, we use the following equation:
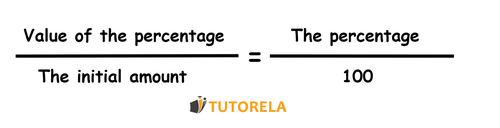
We will always have given values and one unknown that we need to determine.
Pay attention - The data in the question doesn't always direct us to what we're being asked. Therefore, we'll need to use logic and select the values that will provide us with the correct answer.
Practice Percentage
Calculate 35% of 100:
Examples with solutions for Percentage
Calculate 95% of 100:
In order to calculate 15% of 100, start by converting the percentage into a decimal. Convert 15% to a decimal:
Then multiply the decimal by 100 to find the percentage value:
So, 95% of 100 is .
Answer:
Calculate 75% of 100:
In order to calculate 75% of 100, we must first convert the percent into a decimal. Convert 75% to a decimal: .
Then multiply by the whole number: .
Therefore, 75% of 100 is .
Answer:
Calculate 20% of 100:
In order to determine 20% of 100, we begin by converting the percentage into a decimal and then proceed to multiply by the whole number. First, convert 20% to a decimal:
Next, multiply this decimal by 100 to find the percentage of the whole number:
Thus, 20% of 100 is .
Answer:
Calculate 50% of 100:
In order to determine 50% of 100, we first convert the percentage into a decimal. Convert 50% to a decimal: .
Next, multiply the decimal by 100 to get the percentage value: .
Therefore, 50% of 100 is .
Answer:
Calculate 75 over 100 as a percentage:
In order to determine the percentage of 75 out of 100, apply the percentage formula:
Substitute the specific values:
The equation simplifies to:
Therefore, 75 out of 100 is equivalent to 75%.
Answer:
75%