In summary: SAS
It means that:
if two triangles have two equal sides and the angle opposite the larger of these two sides is also equal, then the triangles are congruent.
In summary: SAS
It means that:
if two triangles have two equal sides and the angle opposite the larger of these two sides is also equal, then the triangles are congruent.


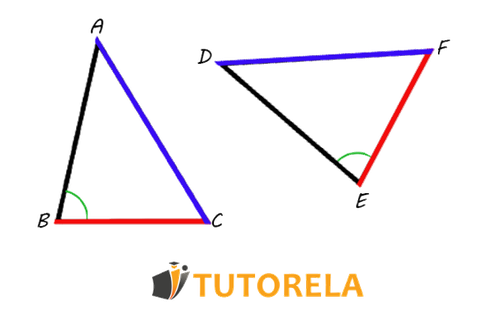
Look at the triangles in the diagram.
Determine which of the statements is correct.
It's time to dive into the fourth theorem of triangle congruence: Side, Side, and the Angle Opposite the Larger of the Two Sides,
or simply put:
SSA
This congruence theorem is practical and straightforward, and it will help us prove triangle congruence under certain simple conditions.
What does the Side, Side, and the Angle Opposite the Larger of the Two Sides congruence theorem say?
If two triangles have two sides of the same length and the angle opposite the larger of these two sides is also the same, then the triangles are congruent.
What does this mean?
Let's see it in an illustration:

If we have:
and also:
That is, the triangles have two equal sides,
and also:
when
That is, the angle opposite to the larger side is also equal.
We can determine that the triangles are congruent according to the SAS (Side-Angle-Side) theorem
Pay attention that, even though it is given in only one triangle
but, since we have a previous statement that says:
and also:
we can determine according to the transitive relation that also:
Therefore, we will determine that:
Notice that we have written the congruence in the correct order.
When
Since the triangles are congruent, identical in their sides and angles, we can say that:
Remember that there must be 3 circumstances and one condition:
The 3 required circumstances are:
The condition:
Look at the triangles in the diagram.
Which of the following statements is true?
Given the triangles in the drawing
According to which theorem, are the triangles congruent?
Look at the triangles in the diagram.
Which of the following statements is true?
Let's look at some ways to do it:
If you found this article interesting, you might also be interested in the following articles:
Congruence Criterion: Side, Angle, Side
Congruence Criterion: Angle, Side, Angle
Congruence Criterion: Side, Side, Side
Style of Writing Formal Proof in Geometry
On the Tutorela blog, you'll find a variety of mathematics articles.
Assignment
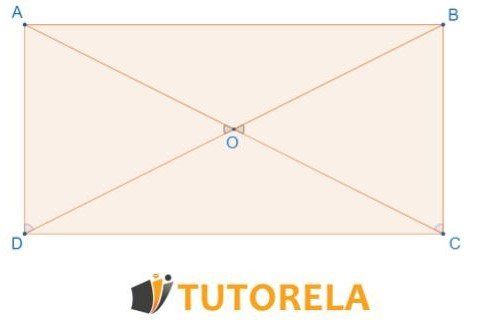
Given: the quadrilateral is a parallelogram.
According to which congruence theorem do the triangles overlap?
Solution
Since the quadrilateral is a rectangle, in the rectangle there are two pairs of opposite equal parallel sides, therefore:
Alternate interior angles are equal because they are between parallel lines, therefore:
Vertically opposite angles are equal, and therefore:
We verify that the triangles are congruent according to the side-angle-angle theorem.
Answer:
Congruent according to ASA (Angle-Side-Angle).
Look at the triangles in the diagram.
Which of the statements is true?
Are the triangles in the image congruent?
Which of the triangles are congruent?
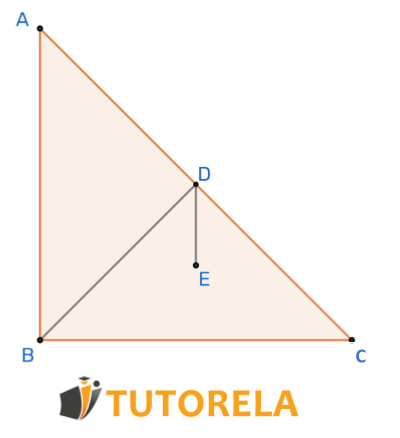
Assignment
Is not a side of any of the triangles?
Solution
If we look at the graphic, we see that from point a line goes to point , therefore is a straight line that is not a side of any triangle in the drawing.
Answer
True
Assignment
In the given drawing:
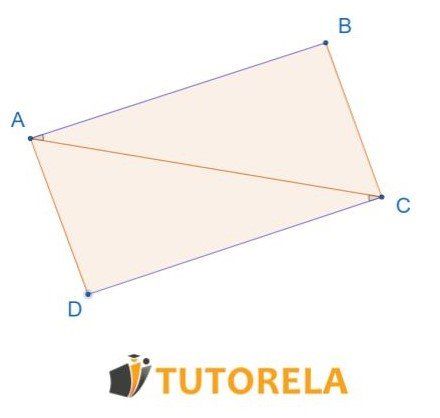
According to which theorem of congruence are the triangles congruent?
Solution
Given that
Given that
is the common side
We verify that the triangles are congruent by side, angle, side
Answer
Congruent by S.A.S
What data must be added for the triangles to be congruent?
What information must be added for the triangles to be congruent?
Are the triangles below congruent?

Prompt
Given rectangle with side measuring cm and side measuring cm.
What is the area of the rectangle?
Solution
The formula to calculate the area of a rectangle is the base times the height; in this case, we replace them
Answer
Assignment
The segments and intersect at point .
According to which theorem of congruence do the triangles match?
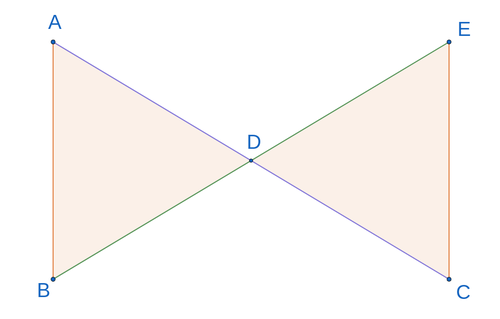
Solution
and
Intersect at a point
intersects
Angles opposite by the vertex
Triangles overlap according to
Answer
Overlapping
Are the triangles congruent?
Are the triangles in the drawing congruent?
Are the triangles congruent?