We'll study the three main congruence criteria. This is the first one of them:
Congruence Criterion: Side, Angle, Side
Side, Angle, Side.
According to this theorem, two triangles are congruent if two of their sides are respectively equal and the angle between them is also equal.
It is important to note that the angle must be between the two equal sides. This criterion cannot be applied if it were a different angle.
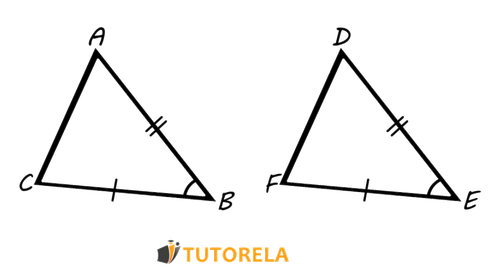
To demonstrate that two triangles are congruent, we can use one of the following postulates:
- SAS - Side, Angle, Side
- ASA - Angle, Side, Angle
- SSS- Side, Side, Side
- HL- Hypotenuse, Leg
Test yourself on side, angle, side!
AB = CD
\( ∢\text{BAC}=∢\text{DCA} \)
According to which theorem are triangles Δ ABC and Δ CDA congruent?
\( \)
Definition of Congruent Triangles
Two triangles are congruent if two sides and the angle between them are equal in measure.
This criterion helps us prove that two angles are congruent.
Attention! The angle must be the one that is between the two equal sides. This theorem cannot be applied if it is another angle.
Example 1 (Side, Angle, Side)
Given two triangles and and the following data:
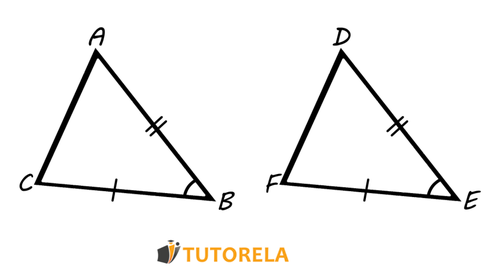
From this, it can be deduced that the triangles and are congruent; therefore, we will write:
according to the Side, Angle, Side (SAS) congruence criterion
AB = CD
\( ∢\text{BAC}=∢\text{DCA} \)
According to which theorem are triangles Δ ABC and Δ CDA congruent?
\( \)
Example 2 - Congruence (Side, Angle, Side)
On side , two triangles have been constructed: triangle and triangle such that:
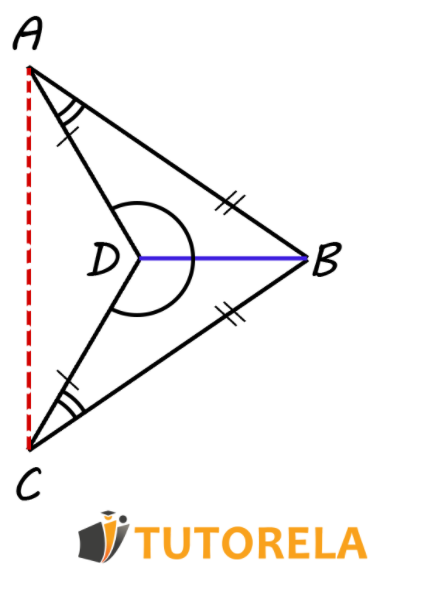
Prove that
Proof:
We will use the criterion that we have learned to prove that triangle and triangle are congruent triangles.
We note that side is common to both triangles (edge)
It is also shown that: (angle)
and that: (edge)
Consequently, we will deduce that according to the Side, Angle, Side (SAS) congruence criterion.
It is crucial to pay attention and write the correct order of the vertices.
After seeing that the triangles are congruent, we can conclude that (Corresponding angles in congruent triangles).
If you're interested in this article, you might also be interested in the following articles:
Congruence Criterion: Angle, Side, Angle
Congruence Criterion: Side, Side, Side
Side, Side and the Angle Opposite the Larger of the Two Sides
Style of Writing a Formal Proof in Geometry
On the Tutorela blog, you'll find a variety of articles about mathematics.
Side-Angle-Side Congruence Exercises
Exercise 1
Given: is the bisector of
To which congruence theorem does belong?
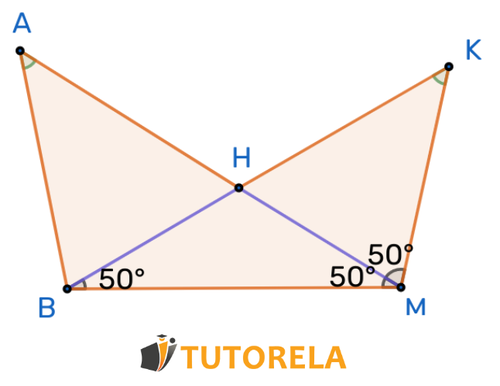
Solution
Common side
Angle is equal to angle given
Angle is given as
Angle is given as
Angle is because is the bisector of
Angle is equal to angle , therefore both are
Angle is equal to angle
If two angles in a triangle are equal, then the third angle will also be equal, and the triangles will overlap according to the Angle-Side-Angle (ASA) congruence theorem
Answer
(Angle-Side-Angle)
AB = CD
\( ∢\text{BAC}=∢\text{DCA} \)
According to which theorem are triangles Δ ABC and Δ CDA congruent?
\( \)
Exercise 2
Prompt
The segments and intersect at point .
Given: Point intersects .
By what criterion of congruence are triangles ?
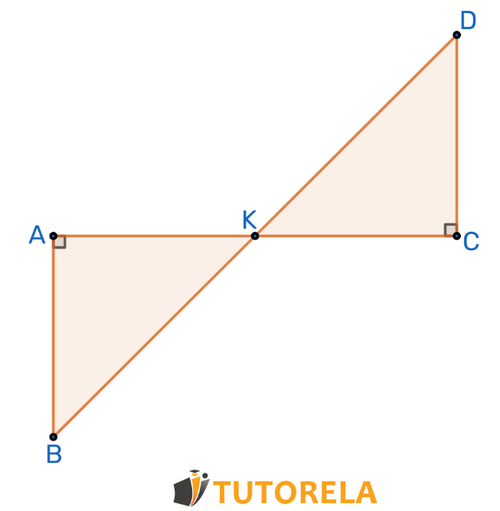
Solution
is perpendicular to
A line perpendicular creates a right angle of degrees, therefore, angle is equal to: degrees
is perpendicular to
A line perpendicular creates a right angle of degrees, therefore, angle is equal to: degrees
From this it follows that the angles
Given point which intersects
Therefore the triangles are congruent according to the criterion (Side, Angle, Side)
Answer
Congruent: (Side, Angle, Side)
Exercise 3
Assignment
In the given figure:
According to which criterion of congruence are ?
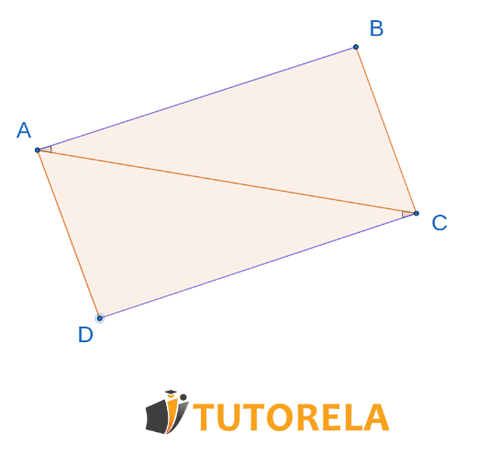
Solution
Given that
Given that the angles
Side is a common side
The triangles are congruent by the theorem (side, angle, side)
Answer
Congruent by (side, angle, side) criterion
AB = CD
\( ∢\text{BAC}=∢\text{DCA} \)
According to which theorem are triangles Δ ABC and Δ CDA congruent?
\( \)
Exercise 4
Task
Are the triangles in the drawing congruent?
If so, explain according to which criterion.
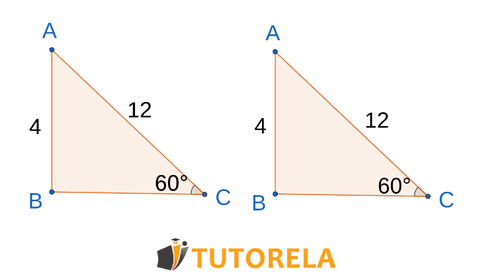
Solution
Angles
The triangles are congruent by the (side, angle, side) congruence criterion.
Answer
Congruent by (side, angle, side)
Exercise 5
Prompt
Are the triangles and congruent?
If so, according to which congruence criterion?
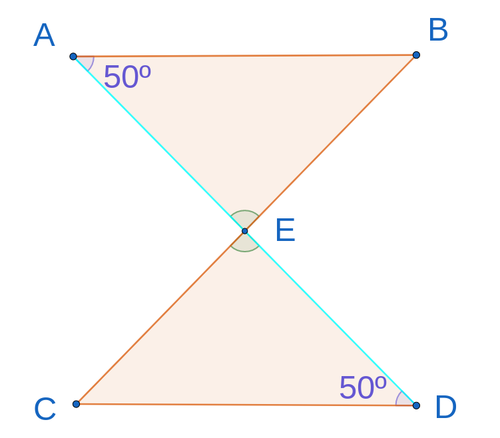
Solution
Given that
angles
angle are vertically opposite angles
The triangles are congruent according to the critterion (angle, angle, side)
Answer
Congruent by (angle, angle, side)
AB = CD
\( ∢\text{BAC}=∢\text{DCA} \)
According to which theorem are triangles Δ ABC and Δ CDA congruent?
\( \)
Exercise 6
Assignment
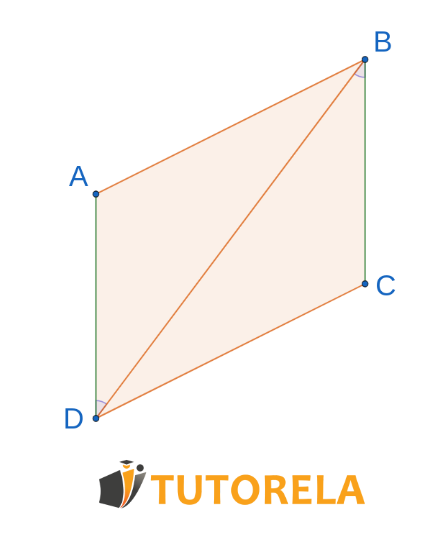
Given the figure:
By which theorem do the triangles coincide?
Solution
Given that
Given that is parallel to
Alternate interior angles between parallel lines are equal
common side
Triangles are congruent according to the criterion.
Answer
According to the criterion.
Review Questions
What is a triangle?
In geometry, a triangle is considered a flat figure with three sides, where the joining of each side, called vertices, forms three angles.
What are congruent triangles?
If two triangles have sides and angles of the same measure, then they are congruent triangles.
What criteria can be used to determine if two triangles are congruent?
There are four criteria to determine whether two triangles are congruent or not, which are as follows:
- SAS - Side, Angle, Side.
- ASA - Angle, Side, Angle.
- SSS - Side, Side, Side.
- SSA - Side, Side, Angle.
What is the Side, Angle, Side criterion?
This criterion tells us that two triangles are congruent when two of their corresponding sides and the angle between them are equal. It should be noted that if the angle analyzed is not the one between these two sides, we cannot use this criterion.
For what types of triangles can we use the congruence criteria?
We can apply the criteria to any type of triangle, whether it's an equilateral triangle, an isosceles triangle, or a scalene triangle.
AB = CD
\( ∢\text{BAC}=∢\text{DCA} \)
According to which theorem are triangles Δ ABC and Δ CDA congruent?
\( \)
Examples with solutions for Side, Angle, Side
Exercise #1
AB = CD
According to which theorem are triangles Δ ABC and Δ CDA congruent?
Video Solution
Answer
Congruent according to L.A.L.
- Congruent Triangles
- Congruence Criterion: Angle, Side, Angle
- Congruence Criterion: Side, Side, Side
- Side, Side, Angle
- Congruence of Right Triangles (using the Pythagorean Theorem)
- The Pythagorean Theorem
- Congruent Rectangles
- Similarity of Triangles and Polygons
- Similarity of Geometric Figures
- Similarity ratio
- Similar Triangles
- Triangle similarity criteria
- Sum of Angles in a Polygon
- Sum of the Interior Angles of a Polygon
- Exterior angles of a triangle
- Sum of the Exterior Angles of a Polygon
- Relationships Between Angles and Sides of the Triangle
- Relations Between The Sides of a Triangle









