Congruence Criterion: Angle, Side, Angle

Given the triangles $Δ ABC$ and $Δ DEF$ such that:
$\sphericalangle A=\sphericalangle D$
$AB = DE$
$\sphericalangle B=\sphericalangle E$

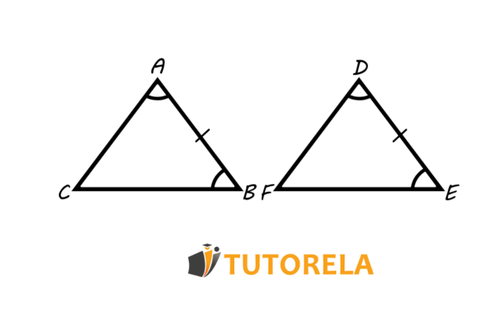
From this, we deduce that the triangles $Δ ABC$ and $Δ DEF$ are congruent, therefore, we will write:

$Δ DEF ≅ Δ ABC$ according to the congruence criterion: Angle, Side, Angle (ASA)

Consequently, we will deduce that:

$BC = EF$

$AC = DF$

since these are corresponding and equal sides in congruent triangles.

Then, we will also deduce that:

\\sphericalangle C=\sphericalangle F\)

since these are corresponding and equal angles in congruent triangles.

Given two parallel lines. The line $AC$ and the line $BD$ pass between them in such a way that they intersect at point $O$. Also, we are informed that $AO = OC$

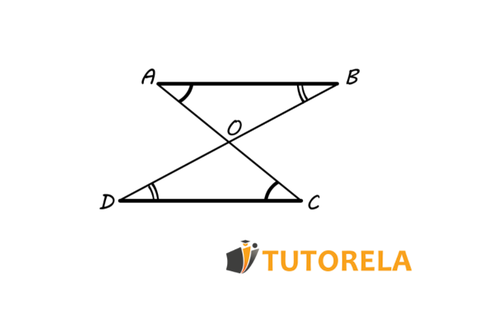
Prove that $AB = DC$

Proof:
First, we must show that triangles $Δ ABO$ and $Δ DOC$ are congruent. We will base this on the previous criterion.

Note that $\sphericalangle AOB = \sphericalangle COD$ (Because they are vertical angles)

Since $AE = EC$ (Side)

Remember that the two given lines are parallel lines.

Therefore, $​​\sphericalangle OAB=\sphericalangle OCD$ since they are alternate interior angles between parallel lines (angle).

We observe that now we have $2$ triangles in which $2$ of their angles and the side included between them are equal.

Consequently, triangles $Δ ABO$ and $Δ DOC$ are congruent

and we write it as $Δ ABO ≅ Δ DOC$ according to the Angle, Side, Angle (ASA) congruence criterion

Therefore, we can deduce that $AB=DC$ (Corresponding sides of congruent triangles).

$QED$

If you're interested in this article, you might also be interested in the following articles:

Congruence Criterion: Side, Angle, Side

Congruence Criterion: Side, Side, Side

Side, Side, and the Angle Opposite the Larger of the Two Sides

How to Write a Formal Proof in Geometry

On the Tutorela blog, you'll find a variety of articles about mathematics.

Assignment

Given that point $K$ bisects $AC$.

and also $∢A=∢C$

According to which theorem of congruence do the triangles $ΔAMK≅ΔCBK$ coincide?

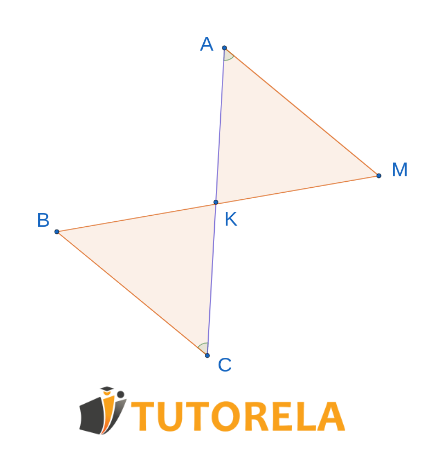
Solution

Given that the angles $A=C$

$AK=KC$

Given that point $K$ cuts $AC$

Angles $AKM=CKB$

Opposite angles by the vertex are equal

The triangles are congruent according to the $A.S.A$ theorem

Answer

$A.S.A$

Assignment

Given: the quadrilateral $ABCD$ is a rectangle.

By which theorem of congruence do the triangles $ΔADO≅ΔCBO$ coincide?

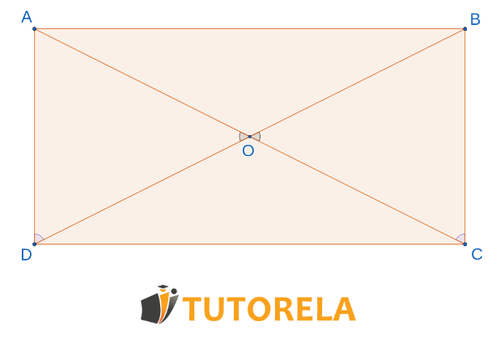
Solution

$BC=AD$

Since the quadrilateral $ABCD$ is a rectangle and in a rectangle there are two pairs of parallel and equal sides

Angles $\sphericalangle BCO=\sphericalangle ADO$ are alternate angles between equal parallel lines.

Angles $O_1=O_2$

opposite angles at the vertex are equal

Therefore, we say that the triangles are congruent according to the $L.A.A$ theorem

Answer

According to the $L.A.A$ theorem

Assignment

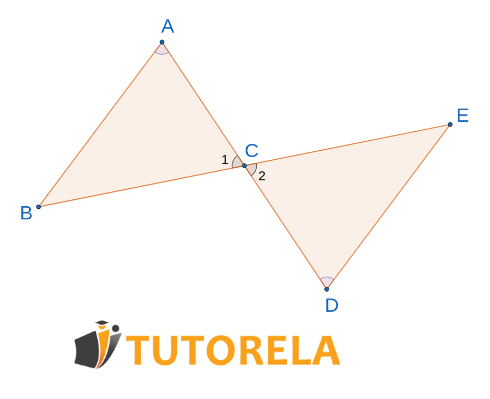
In the given figure: $DE || AB$

and point $C$ bisects segment $BE$.

According to which theorem of congruence do the triangles match?

$ΔABC≅ΔDEC$

Solution

Given that $DE$ is parallel to $AB$

Angles $D=A$

Alternate angles are equal between parallel lines

$BC=CE$ Point $C$ bisects the line $BE$

Angles $C_1=C_2$

Vertex opposite angles

Triangles congruent according to the superposition theorem $L.A.A$

Answer

Superimposed according to $L.A.A$

Assignment

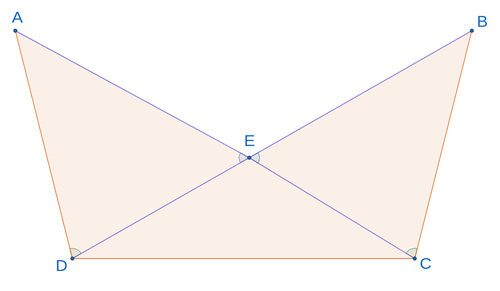
Given the isosceles triangle $ΔEDC$.

$∢ADE=∢BCE$

$AC=BD$

According to which theorem of congruence do the triangles coincide?

$ΔADE≅ΔBCE$

Solution

Triangle $ΔEDC$ is an isosceles triangle

$DE=EC$

In an isosceles triangle, two sides are equal

Angles $D=C$ given

angles $EDC=ECD$ the base angles of an isosceles triangle are equal

angles $ADE=BCE$

$\sphericalangle D-\sphericalangle EDC=\sphericalangle C-\sphericalangle ECD$

Subtraction of angles

$\sphericalangle E_1=\sphericalangle E_2$

Triangles are congruent according to the $ASA$ theorem

Answer

$ASA$

Assignment

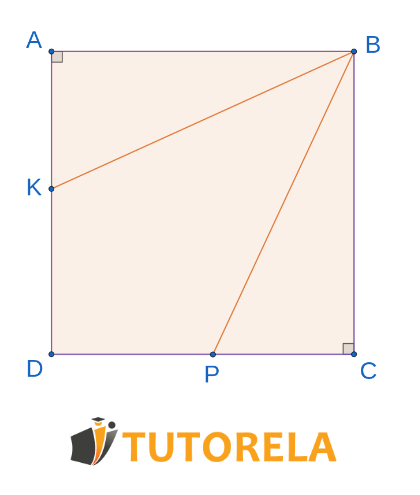
Given: quadrilateral $ABCD$ square.

And within it is enclosed the kite $KBPD$.

According to which theorem of congruence do the triangles $ΔBAK≅ΔBCP$ coincide?

Solution

$ABCD$ is a square

$AB=BC$

In a square all sides are equal

Given that $KBPD$ is a kite

$BK=BP$

In a kite two pairs of adjacent sides are equal

$\sphericalangle C=\sphericalangle A$

Equal angles in a square are $90°$ degrees

$\sphericalangle BPC=\sphericalangle BKA$

The angles of the kite are equal $\sphericalangle K=\sphericalangle P$

therefore $180° -\sphericalangle K=180° -\sphericalangle P$

$\sphericalangle ABK=\sphericalangle PBC$

if two angles are equal then the third is also equal

The triangles are congruent according to $S.A.S$

Answer

$S.A.S$

What is a criterion in geometry?

In mathematics, a criterion is a judgment or a guideline that allows us to determine certain characteristics depending on the case or topic being studied. In the case of geometry, it allows us to judge certain characteristics for given figures.

What is the triangle congruence criterion?

There are $4$ triangle congruence criteria, which help us determine when two triangles are congruent, that is, they help us determine when two triangles have the same dimensions and corresponding angles, thus having the same shape and side measurements regardless of the orientation of these triangles.

What is the AAS criterion?

We say that two triangles are congruent with the AAS criterion when two of their angles and a non-included side are congruent.

What is the angle-side-angle criterion?

This criterion tells us that two triangles are congruent when two angles and the side between them are congruent.

How do you determine the criterion of a triangle?

This depends on the corresponding angles and sides of both triangles.

For example, given two triangles:

If we have three corresponding sides of two triangles that are congruent, then we are talking about the SSS criterion.

If it is found that the two angles and the included side between the corresponding angles are congruent, we refer to the ASA criterion.

When observing that two of their angles and the non-included side are congruent respectively, then we are discussing the AAS criterion.

And finally, when two pairs of corresponding sides and the included angle between these sides are congruent, it will be the SAS criterion.

Based on this, we can determine which congruence criterion we are referring to and deduce whether or not they are congruent triangles.