Sum and Difference of Angles Practice Problems & Solutions

Master angle relationships with practice problems on corresponding angles, alternate angles, adjacent angles, and parallel lines. Step-by-step solutions included.

📚Master Angle Relationships Through Targeted Practice

Identify and calculate corresponding angles between parallel lines
Solve for unknown angles using alternate angle properties
Apply adjacent angle relationships to find missing measurements
Work with vertically opposite angles in intersection problems
Calculate angles in triangles using parallel line theorems
Distinguish between acute, obtuse, right, and straight angles in complex figures

Understanding Types of Angles

Complete explanation with examples

What is an angle?

Definition: Angles are created at the intersection between two lines. As seen in the following illustration

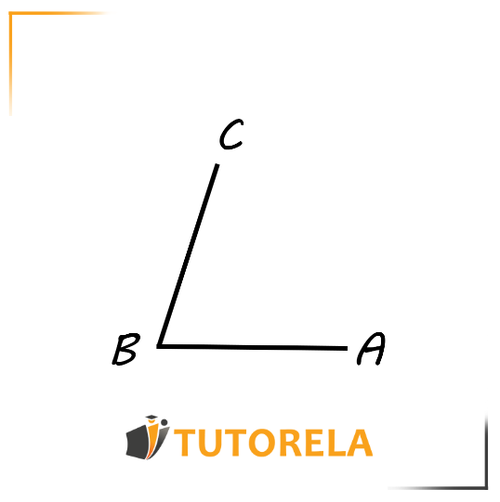
The angle in the illustration is called $AB$ . We could also call it angle $\sphericalangle ABC$ . The important thing is that the middle letter is the one at the intersection of the lines.

For example, in this case:

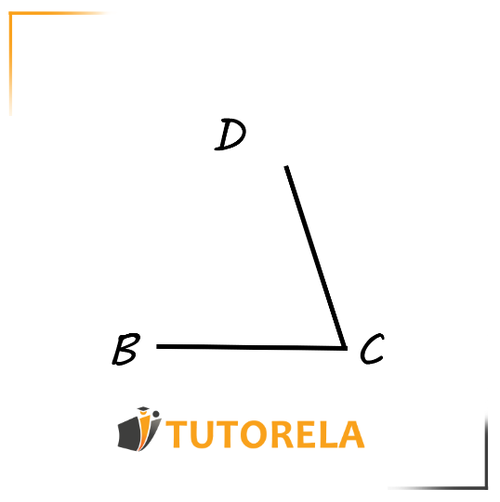
The angle is $\sphericalangle BCD$ or $\sphericalangle DCB$ . Both notations are correct for the same angle.

We usually mark the angle with an arc as follows:

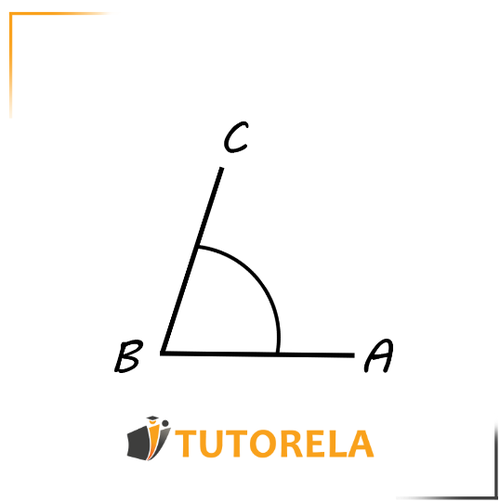
The marked angle is $∡ABC$ . Sometimes we will denote angles using Greek letters, for example:

$α$ or $β$

Before the name of the angle, we should note the angle symbol, like this:

$∡$

Together it looks like this:

$∡CBA$ or $∡α$

Next, we will delve into the size of angles, the different types, and those that are created when a line intersects two parallel lines.

Detailed explanation

Practice Types of Angles

Test your knowledge with 28 quizzes

Find the measure of the angle $\alpha$

Examples with solutions for Types of Angles

Step-by-step solutions included

Exercise #1

Indicates which angle is greater

Step-by-Step Solution

Answer B is correct because the more closed the angle is, the more acute it is (less than 90 degrees), meaning it's smaller.

The more open the angle is, the more obtuse it is (greater than 90 degrees), meaning it's larger.

Answer:

Video Solution

Exercise #2

Indicates which angle is greater

Step-by-Step Solution

In drawing A, we can see that the angle is an obtuse angle, meaning it is larger than 90 degrees:

While in drawing B, the angle is a right angle, meaning it equals 90 degrees:

Therefore, the larger angle appears in drawing A.

Answer:

Video Solution

Exercise #3

Which angle is greatest?

Step-by-Step Solution

In drawing A, we can see that the angle is more closed:

While in drawing B, the angle is more open:

In other words, in diagram (a) the angle is more acute, while in diagram (b) the angle is more obtuse.

Remember that the more obtuse an angle is, the larger it is.

Therefore, the larger of the two angles appears in diagram (b).

Answer:

Video Solution

Exercise #4

What is the size of angle ABC?

Step-by-Step Solution

In order to calculate the value of angle ABC, we must calculate the sum of all the given angles.

That is:

$ABC=60+50$

$ABC=110$

Answer:

110

Video Solution

Exercise #5

Find the measure of the angle $\alpha$

Step-by-Step Solution

It is known that the sum of angles in a triangle is 180 degrees.

Since we are given two angles, we can calculate $a$

$94+92=186$

We should note that the sum of the two given angles is greater than 180 degrees.

Therefore, there is no solution possible.

Answer:

There is no possibility of resolving

Video Solution

Frequently Asked Questions

Everything you need to know about Types of Angles

What are corresponding angles and how do I identify them?

Corresponding angles are formed when a transversal cuts two parallel lines, positioned on the same side of the transversal and at the same level relative to each parallel line. They are always equal in measure. Look for angles that occupy the same relative position at each intersection point.

How do I solve problems involving alternate angles?

Alternate angles are equal when formed by parallel lines and a transversal, but they're on opposite sides of the transversal and at different levels. To solve: 1) Identify the parallel lines, 2) Locate the transversal, 3) Find angles on opposite sides that aren't at the same level, 4) Set them equal and solve.

What's the difference between adjacent angles and vertically opposite angles?

Adjacent angles share a common vertex and side, and their measures add up to 180° when they form a straight line. Vertically opposite angles are formed by two intersecting lines and face each other across the intersection point - they are always equal in measure.

How do I calculate missing angles in triangles with parallel lines?

Use these steps: 1) Identify corresponding or alternate angles created by parallel lines, 2) Transfer known angle measures using these relationships, 3) Apply the triangle angle sum theorem (angles total 180°), 4) Set up an equation and solve for the unknown angle.

What are the key angle relationships I need to memorize?

Essential relationships include: • Corresponding angles are equal (parallel lines) • Alternate angles are equal (parallel lines) • Adjacent angles sum to 180° on a straight line • Vertically opposite angles are equal • Triangle angles sum to 180° • Right angles measure exactly 90°

How do I know when to use angle properties with parallel lines?

Look for these indicators in problems: parallel line symbols (∥), statements mentioning 'parallel lines,' diagrams showing lines that don't intersect, or problems asking about 'corresponding' or 'alternate' angles. These signal that you should apply parallel line angle theorems.

What's the easiest way to remember acute, right, obtuse, and straight angles?

Use this memory system: Acute angles are 'cute and small' (less than 90°), Right angles form perfect corners (exactly 90°), Obtuse angles are 'obese and big' (between 90° and 180°), Straight angles form straight lines (exactly 180°). Visual practice helps reinforce these concepts.

How do I solve complex angle problems step by step?

Follow this systematic approach: 1) Read the problem carefully and identify given information, 2) Draw or label the diagram clearly, 3) Identify which angle relationships apply, 4) Write equations based on these relationships, 5) Solve algebraically, 6) Check your answer makes geometric sense.

Continue Your Math Journey

Master Types of Angles first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Sides, Vertices, and Angles Sum and Difference of Angles Sum of Angles in a Polygon The Sum of the Interior Angles of a Triangle Exterior angles of a triangle

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Angle bisector Applying the formula Calculate Angles in Quadrilaterals Finding the size of angles in a triangle Generate a random angle Identifying and defining elements Identify the greater value Is it possible...? Isosceles triangle Using angles in a triangle Using parallel lines Using quadrilaterals Using ratios for calculation Using variables

Sum and Difference of Angles Practice Problems & Solutions

Understanding Types of Angles

What is an angle?

Practice Types of Angles

Examples with solutions for Types of Angles

Frequently Asked Questions

What are corresponding angles and how do I identify them?

How do I solve problems involving alternate angles?

What's the difference between adjacent angles and vertically opposite angles?

How do I calculate missing angles in triangles with parallel lines?

What are the key angle relationships I need to memorize?

How do I know when to use angle properties with parallel lines?

What's the easiest way to remember acute, right, obtuse, and straight angles?

How do I solve complex angle problems step by step?

More Types of Angles Questions