We can add angles and get the result of their sum, and we can also subtract them to find the difference between them.
Even if the angles don't have any numbers, we'll learn how to represent their sum or difference and arrive at the correct result.
Sum and Difference of Angles Practice Problems & Worksheets
Master angle addition and subtraction with step-by-step practice problems. Learn to find unknown angles using common vertex relationships and triangle properties.
📚Practice Sum and Difference of Angles Problems
- Calculate angle sums when angles share a common vertex
- Find missing angles by subtracting known angles from larger angles
- Apply angle relationships in triangles to solve for unknown values
- Work with parallel lines and corresponding angle properties
- Solve multi-step problems involving angle addition and subtraction
- Master proper angle notation and naming conventions
Understanding Sum and Difference of Angles
Complete explanation with examples
Sum and Difference of Angles
Angle Sum
To find the sum of angles, they must have a common vertex.
Difference Between Angles
Just as we have added angles, we can also subtract one from another.
We can say that:
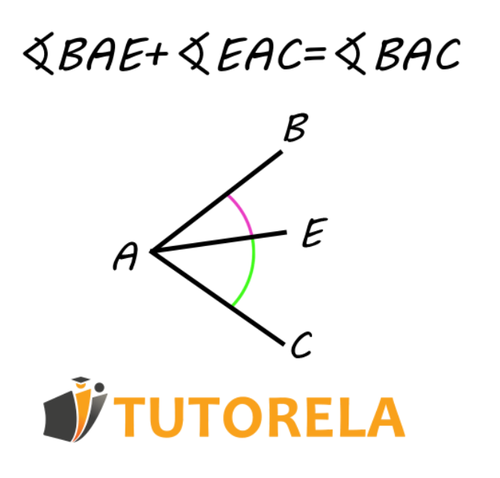
Practice Sum and Difference of Angles
Test your knowledge with 28 quizzes
Find the measure of the angle \( \alpha \)
Examples with solutions for Sum and Difference of Angles
Step-by-step solutions included
Exercise #1
Indicates which angle is greater
Step-by-Step Solution
In drawing A, we can see that the angle is an obtuse angle, meaning it is larger than 90 degrees:
While in drawing B, the angle is a right angle, meaning it equals 90 degrees:
Therefore, the larger angle appears in drawing A.
Answer:
Video Solution
Exercise #2
Indicates which angle is greater
Step-by-Step Solution
Note that in drawing B, the two lines form a right angle, which is an angle of 90 degrees:
While the angle in drawing A is greater than 90 degrees:
Therefore, the angle in drawing A is larger.
Answer:
Video Solution
Exercise #3
Which angle is greater?
Step-by-Step Solution
The angle in diagram (a) is more acute, meaning it is smaller:
Conversely, the angle in diagram (b) is more obtuse, making it larger.
Answer:
Video Solution
Exercise #4
Indicates which angle is greater
Step-by-Step Solution
Note that in drawing A, the angle is a straight angle equal to 180 degrees:
While in drawing B, we are given a right angle, equal to 90 degrees:
Therefore, the angle in drawing A is larger.
Answer:
Video Solution
Exercise #5
Which angle is greatest?
Step-by-Step Solution
In drawing A, we can see that the angle is more closed:
While in drawing B, the angle is more open:
In other words, in diagram (a) the angle is more acute, while in diagram (b) the angle is more obtuse.
Remember that the more obtuse an angle is, the larger it is.
Therefore, the larger of the two angles appears in diagram (b).
Answer:
Video Solution
Frequently Asked Questions
How do you add angles that share a common vertex?
+When angles share a common vertex, you can add their measures directly. For example, if ∠BAE = 30° and ∠EAC = 35°, then ∠BAC = 30° + 35° = 65°. The key is that the angles must be adjacent and share the same vertex point.
What is the rule for subtracting angles?
+To subtract angles, you take a larger angle and subtract a smaller angle that is contained within it. If ∠BAC = 65° and ∠BAE = 30°, then ∠EAC = 65° - 30° = 35°. Remember: the whole angle equals the sum of its parts.
How do you find unknown angles in triangles using angle sum?
+Use the fact that all angles in a triangle sum to 180°. Steps: 1) Add the two known angles, 2) Subtract this sum from 180°, 3) The result is your unknown angle. For example: if two angles are 60° and 45°, the third angle = 180° - 60° - 45° = 75°.
What are corresponding angles in parallel lines?
+Corresponding angles are angles in the same relative position when a transversal crosses two parallel lines. They are always equal in measure. This property helps solve angle problems involving parallel lines and transversals.
How do you name angles correctly in sum and difference problems?
+Angle notation uses three points: vertex in the middle, with one point on each ray. ∠BAC means the angle at vertex A, with rays extending to points B and C. Proper naming is crucial for identifying which angles to add or subtract.
What is the complementary angle rule for 180 degrees?
+Adjacent angles that form a straight line sum to 180°. If one angle is 120°, its adjacent angle is 180° - 120° = 60°. This supplementary relationship is essential for solving many angle problems.
How do you solve for x in angle addition problems?
+Set up an equation based on angle relationships. For triangles, use angle sum = 180°. For straight lines, use adjacent angles = 180°. Substitute known values and solve algebraically for the unknown variable x.
What are the most common mistakes in angle sum and difference?
+Common errors include: 1) Mixing up angle names and measuring wrong angles, 2) Forgetting that triangle angles sum to 180°, 3) Not recognizing adjacent angles on straight lines, 4) Incorrect substitution in algebraic equations. Always double-check your angle identification.