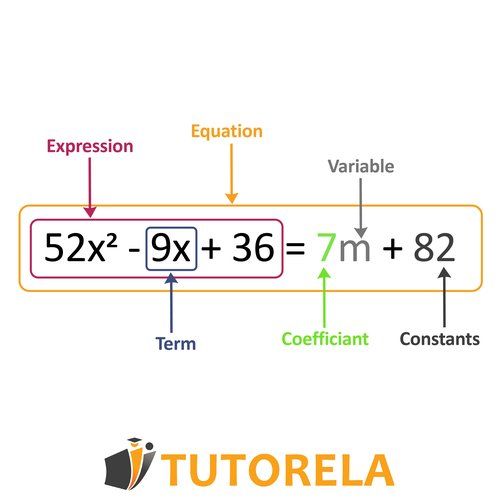
A variable is a specific symbol like a Latin letter – // that can change and represent a quantity/value.

A variable is a specific symbol like a Latin letter – // that can change and represent a quantity/value.

\( 5x=1 \)
What is the value of x?
A variable is a certain symbol like a Latin letter – // that can change and take on a different value each time.
The meaning of the variable is to symbolize something for us – quantity, price, an element within a set, or some value.
The variable can appear in a function or as part of some expression and can also be called an unknown or a parameter.
A variable can be dependent or independent.
A dependent variable is one that depends on something – for example, in a function, which will depend on the we substitute for it.
An independent variable is one that does not depend on anything - usually (it can have a certain range of values) and it will ultimately determine the value of the dependent variable.
Important to know –
Although the variable changes and can take on a different number each time, if the same variable appears several times in the same expression or function, it will be identical in all its occurrences in the function.
Let's see an example:
Given the following function:
Solution:
\( 5x=0 \)
\( 14x+3=17 \)
\( x=\text{?} \)
Solve the following problem:
\( 2x+7-5x-12=-8x+3 \)
Sometimes, we encounter word problems where we are asked to find the value of something specific, like the price of a shirt, the number of slices of cake, or the number of children.
We can take the data from the question and turn it into an algebraic equation using variables.
When we have an algebraic equation composed of various variables based on the data in the question, we can easily solve the word problem.
Let's see an example:
Advanced word problem with variables –
Saar went to the nearby mall and decided to buy shirts, pair of pants, and packs of cards.
It is known that a shirt costs and the price of the pants is times the price of the shirt.
It is also known that the price of a pack of cards is half the price of the pants.
Additionally, Saar paid dollars for parking.
Solution:
1. We will represent the data of the question using variables:
Price of a shirt = known according to the data of the question
Price of pants =
According to the question data, it is known that the price of pants is times higher than the price of the shirt.
Price of a pack of cards =
If the price of the pants is , and the price of a pack of cards is half the price of the pants, then the price of the pack of cards is divided by .
2. If
The price of the pants is
90 $
And the price of a pack of cards is:
3. To know how much Sa'ar paid in total at the mall, we need to build an equation:
Note that it is given that:
Sa'ar decided to buy shirts, pair of pants, and packs of cards and paid an additional 8 $ for parking.
Therefore, the equation will be:
Saar spent 293 $ in total during the entire visit to the mall, including parking.
\( 5x=1 \)
What is the value of x?
\( 5x=0 \)
\( 14x+3=17 \)
\( x=\text{?} \)
What is the value of x?
To solve the equation , we need to isolate . Here are the steps:
Therefore, the solution to the equation is .
The correct answer choice is:
To solve the equation for , we will use the following steps:
Let's perform the calculation as outlined in Step 2:
Divide both sides by 5 to isolate :
Simplifying, this gives:
Therefore, the solution to the equation is .
The correct answer is option 4: .
To solve the equation , we need to find the value of that satisfies the equation.
Step 1: Isolate the term containing by subtracting 3 from both sides of the equation:
This simplifies to:
Step 2: Solve for by dividing both sides by 14:
Which simplifies to:
Therefore, the solution to the equation is .
Solve the following problem:
In order to solve this exercise, we first need to identify that we have an equation with an unknown.
To solve such equations, the first step will be to arrange the equation so that on one side we have the numbers and on the other side the unknowns.
First, we'll move all unknowns to one side.
It's important to remember that when moving terms, the sign of the number changes (from negative to positive or vice versa).
Now we'll do the same thing with the regular numbers.
In the next step, we'll calculate the numbers according to the addition and subtraction signs.
At this stage, we want to reach a state where we have only one , not ,
Thus we'll divide both sides of the equation by the coefficient of the unknown (in this case - 5).