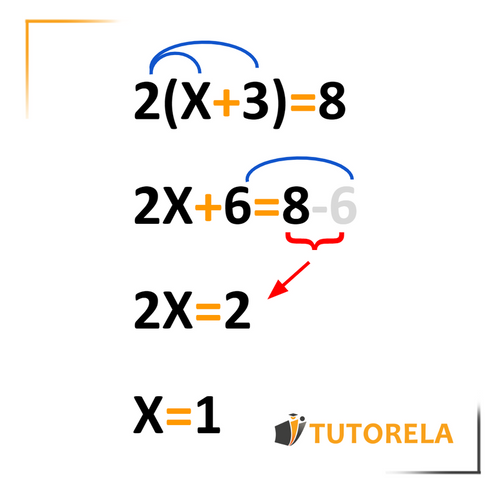
Solving Equations Using the Distributive Property

Solving an equation using the distributive property is related to the need to open the parentheses as the first step to then be able to simplify similar members. When an equation contains one or more pairs of parentheses, we must start by opening them all and then proceed to the next phase.

Below, we provide you with some examples where this method is applied.

$2\left(X+3\right)=8$

In this equation, we can clearly see some parentheses. To start, we must open them (that is, apply the distributive property) and then we can proceed with the following phases of the exercise.

$2X+6=8$

$2X=2$

$X=1$

The result of the equation is $1$ .

Solving equations using the distributive property

Detailed explanation

Start practice

Test yourself on solving quadratic equations using factoring!

Solve x:

$$ 5(x+3)=0 $$

Practice more now

Another example

$5\left(X+2\right)=3\left(X+4\right)$

In this equation, we clearly see that there are two pairs of parentheses, one on each side. To begin, we must open them (that is, apply the distributive property) and then we can proceed with the following phases of the exercise.

$5X+10=3X+12$

$2X=2$

$X=1$

The result of the equation is $1$ .

If this article interested you, you might also be interested in the following articles

On the Tutorela website, you will find a wide variety of articles about mathematics

Examples and exercises with solutions for solving equations using the distributive property

Exercise #1

Solve x:

$5(x+3)=0$

Video Solution

Step-by-Step Solution

We open the parentheses according to the formula:

$a(x+b)=ax+ab$

$5\times x+5\times3=0$

$5x+15=0$

We will move the 15 to the right section and keep the corresponding sign:

$5x=-15$

Divide both sections by 5

$\frac{5x}{5}=\frac{-15}{5}$

$x=-3$

Answer

$-3$

Exercise #2

Solve for x:

$7(-2x+5)=77$

Video Solution

Step-by-Step Solution

To open parentheses we will use the formula:

$a(x+b)=ax+ab$

$(7\times-2x)+(7\times5)=77$

We multiply accordingly

$-14x+35=77$

We will move the 35 to the right section and change the sign accordingly:

$-14x=77-35$

We solve the subtraction exercise on the right side and we will obtain:

$-14x=42$

We divide both sections by -14

$\frac{-14x}{-14}=\frac{42}{-14}$

$x=-3$

Answer

-3

Exercise #3

Solve for x:

$-3(\frac{1}{2}x+4)=\frac{1}{2}$

Video Solution

Step-by-Step Solution

We open the parentheses on the left side by the distributive property and use the formula:

$a(x+b)=ax+ab$

$-\frac{3}{2}x-12=\frac{1}{2}$

We multiply all terms by 2 to get rid of the fractions:

$-3x-12\times2=1$

$-3x-24=1$

We will move the minus 24 to the right section and keep the corresponding sign:

$-3x=24+1$

$-3x=25$

Divide both sections by minus 3:

$\frac{-3x}{-3}=\frac{25}{-3}$

$x=-\frac{25}{3}$

Answer

$-\frac{25}{3}$

Exercise #4

Solve for x:

$8(x-2)=-4(x+3)$

Video Solution

Step-by-Step Solution

To open parentheses we will use the formula:

$a(x+b)=ax+ab$

$(8\times x)+(8\times-2)=(-4\times x)+(-4\times3)$

We multiply accordingly

$8x-16=-4x-12$

In the left section we enter the elements with the X and in the right section those without the X, remember to change the plus and minus signs as appropriate when transferring:

$8x+4x=-12+16$