Solution by all methods
First-degree equation in one variable – solving by all methods
A first-degree equation is an equation where the highest power is and there is only one variable .
Solving an Equation by Adding/Subtracting from Both Sides If the number is next to with a plus, we need to subtract it from both sides.
If the number is next to with a minus, we need to add it to both sides.
Solving an Equation by Multiplying/Dividing Both Sides We will need to multiply or divide both sides of the equations where there is a coefficient for .
Solving an Equation by Combining Like Terms Move all the s to the right side and all the numbers to the left side.
Solving an equation using the distributive property We will solve according to the distributive property
Test yourself on solving equations using all methods!
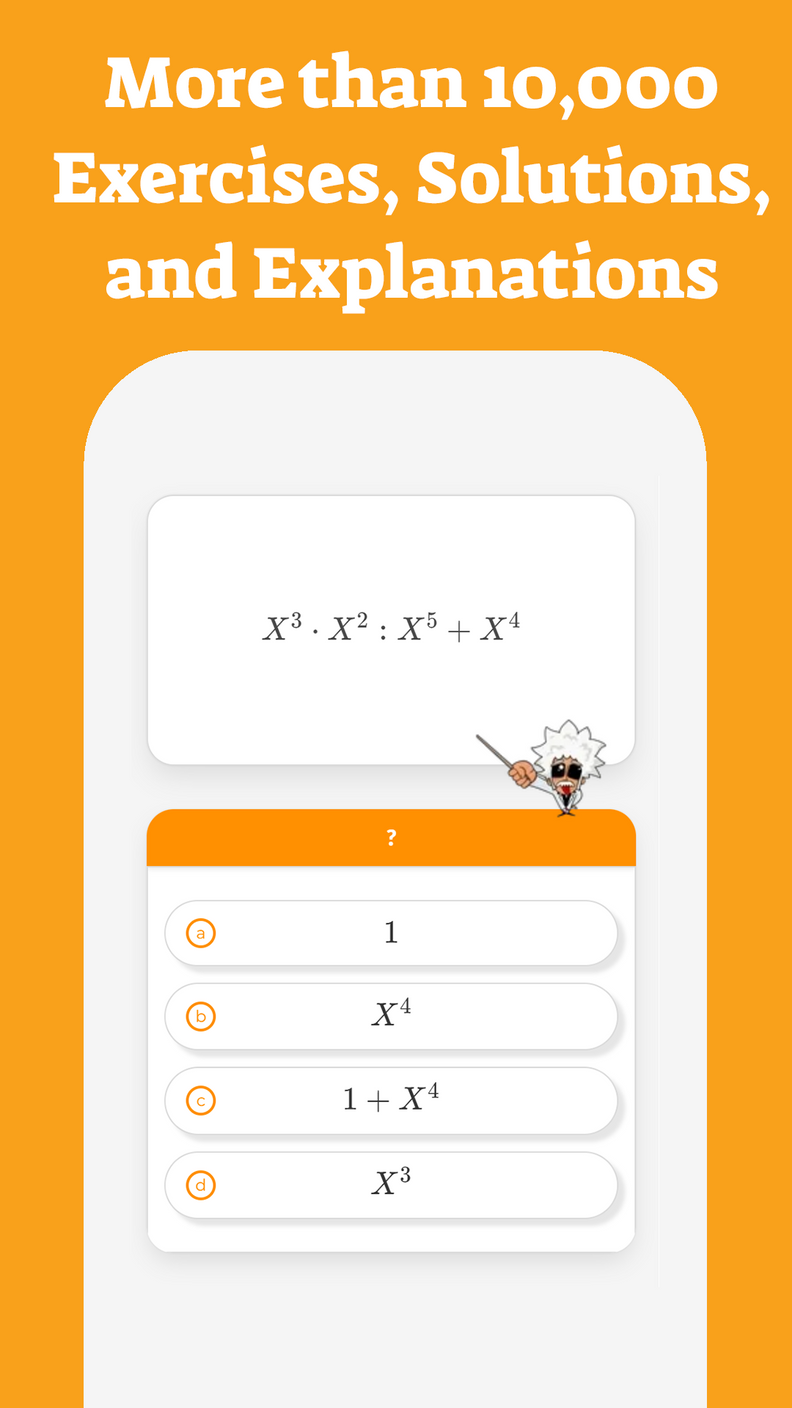
Solve for x:
\( 2(4-x)=8 \)
Solving a first-degree equation using all methods.
What is a first-degree equation with one variable?
First of all, it's worth remembering that a first-degree equation with one variable is essentially an equation where the highest "power" is . This means it is not an equation with a number or variable squared or raised to higher powers. Additionally, it contains only one variable – usually . The may appear multiple times in the exercise, but it will always be the same and not and , for example.
The solution to these equations is simply to find and understand what it equals.
Examples of first-degree equations with one variable:
And now? On to the solution methods!
Solving an equation by adding/subtracting from both sides
The logic in this solution is simply to keep the variable on one side of the equation and the numbers on the other side of the equation. Essentially, if we subtract from both sides or add to both sides, it's exactly like moving a term to the other side!
If the number is next to with a plus, we will need to subtract it from both sides.
If the number is next to with a minus, we will need to add it to both sides.
For example:
Solution:
The goal is to leave only the on one side. This means we need to get rid of the .
To get rid of it, we need to subtract from both sides. We get:
Another exercise:
Solution:
To isolate , we need to add to both sides and subtract from both sides.
We get
\( x+7=14 \)
\( x=\text{?} \)
Solve for X:
\( 5x=25 \)
Solve for X:
\( x + 8 = 10 \)
Solving an equation by multiplying/dividing both sides
We will need to multiply or divide both sides of the equations where there is a coefficient for .
First, we want to reach a situation where only the is on one side and all the numbers are on the other side. Then we want to reach a situation where has no coefficient.
When the coefficient is multiplied with , we will need to divide the equation on both sides.
When the variable is in the numerator, we will need to multiply both sides to eliminate the fraction.
For example:
Solution:
First, we will move all the numbers to one side, we need to subtract from both sides.
We get:
Now, to leave without a coefficient, we need to divide both sides by the coefficient of - .
We get:
Another exercise:
Solution:
To eliminate the fraction, we need to multiply both sides by to cancel the denominator.
We get:
Solving an equation by combining like terms
In this solution, we need to move all the numbers with the variable to one side and all the numbers without the variable to the other side. Of course, we will act according to the addition and subtraction signs accordingly.
Remember – every expression that changes sides changes its sign.
For example:
Solution:
Move all the s to the left side and all the numbers to the right side.
We get:
Now divide both sides by and we get:
Solve for X:
\( \frac{1}{3}x=9 \)
Find the value of the parameter X:
\( x+5=8 \)
\( x+x=8 \)
Solving an equation using the distributive property.
The distributive law will help us eliminate parentheses and simplify multiplication into simple addition and subtraction exercises.
Let's recall the distributive law:
And the expanded distributive law:
In equations with a first degree and one variable, we can apply the distributive law.
For example:
Solution:
According to the distributive law, we get:
Rearranging the terms, we get:
Solve for X:
\( x + 7 = 12 \)
Solve for X:
\( 5-x=4 \)
Solve for x:
\( 7(-2x+5)=77 \)
Examples with solutions for Solving Equations Using All Methods
Exercise #1
Solve for x:
Video Solution
Step-by-Step Solution
To solve this equation, follow these steps:
Step 1: Apply the distributive property to the equation:
Step 2: Simplify the equation:
The equation now becomes:
Step 3: Isolate the variable by simplifying the equation:
First, subtract 8 from both sides:
This simplifies to:
Step 4: Solve for by dividing both sides by -2:
Therefore, the solution to the equation is .
Answer
0
Exercise #2
Video Solution
Step-by-Step Solution
To solve the equation , we aim to find the value of by isolating it on one side.
- Step 1: Identify the current equation: .
- Step 2: To isolate , perform the inverse operation. Subtract 7 from both sides to maintain equality.
- Step 3: Simplify both sides: .
- Step 4: This simplifies to .
Therefore, we have found that the solution to the equation is , which matches the given answer choice 2.
Answer
7
Exercise #3
Solve for X:
Video Solution
Step-by-Step Solution
To solve the equation , we will isolate using division:
- Divide both sides of the equation by 5:
After performing the division, we get:
Thus, the solution to the equation is .
Answer
5
Exercise #4
Solve for X:
Video Solution
Step-by-Step Solution
To solve for , start by isolating on one side of the equation:
Subtract 8 from both sides:
simplifies to
.
Answer
2
Exercise #5
Solve for X:
Video Solution
Step-by-Step Solution
To solve the equation , we need to isolate the variable . To accomplish this, we can multiply both sides of the equation by 3, the reciprocal of .
Step-by-step solution:
- Step 1: Multiply both sides by 3.
- Step 2: Simplify the left side.
This gives us , since . - Step 3: Conclude that .
Therefore, the solution to the equation is . This matches choice number 1 from the provided options.
Answer
27
More Questions
Solving an Equation by Multiplication/ Division
Solving Equations Using All Methods
Solving Equations by using Addition/ Subtraction
Simplifying and Combining Like Terms
Solving Quadratic Equations using Factoring
- Equivalent Equations
- Solving Equations Using the Distributive Property
- Solving Equations by Adding or Subtracting the Same Number from Both Sides
- Solving Equations by Multiplying or Dividing Both Sides by the Same Number
- Solving Equations by Simplifying Like Terms
- Functions for Seventh Grade
- Increasing and Decreasing Intervals (Functions)
- Increasing functions
- Decreasing function
- Constant Function
- Decreasing Interval of a function
- Increasing Intervals of a function
- Domain of a Function
- Indefinite integral
- Inputing Values into a Function
- Rate of Change of a Function
- Variation of a Function
- Rate of change represented with steps in the graph of the function
- Rate of change of a function represented graphically
- Constant Rate of Change
- Variable Rate of Change
- Rate of Change of a Function Represented by a Table of Values
- Ways to Represent a Function
- Representing a Function Verbally and with Tables
- Graphical Representation of a Function
- Algebraic Representation of a Function
- Notation of a Function
- Solution by all methods