Solution of an equation

The solution of an equation is, in fact, a numerical value that, if we place it in place of the unknown (or the variable), we will achieve equality between the two members of the equation, that is, we will obtain a "true statement". In first degree equations with one unknown, there can only be one solution.

Example:

$X - 1 = 5$

This is an equation with one unknown or variable indicated by the letter $X$ . The equation is composed of two members separated by the use of the equal sign $=$ . The left member is everything to the left of the sign $=$ , and the right member is everything to the right of the sign.

Our goal is to isolate the variable (or clear the variable) $X$ so that only it remains in one of the members of the equation. In this way we will discover its value. In this article we will learn how to use the four mathematical operations(addition, subtraction, multiplication and division) to isolate the variable $X$ .

Detailed explanation

Start practice

Test yourself on linear equations!

Solve the equation

$$ 5x-15=30 $$

Practice more now

In this article we will get to know the equations and learn simple ways to solve them.

We will now look at equations with only one unknown

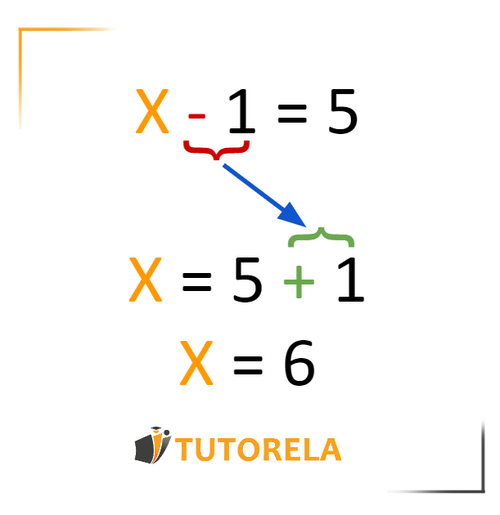
For example

Let's go back to the equation of the previous example:

$X-1 = 5$

We want to isolate $X$ . To do this we will add $1$ to both members of the equation.

We will write it like this:

$X-1 = 5$

We will obtain:

$x-1 + 1 = 5 + 1$

That is:

$X = 6$

And, this is the solution to our equation. We can always check if we got it right by putting our answer in the original equation. Let's put $X=6$ into the equation

$X-1 = 5$

and we get

$6-1 = 5$

$5=5$

this is a true statement, $5$ really equals $5$ , i.e., our solution is correct.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

$$ 4x:30=2 $$

Question 2

Solve the equation

$$ 7x+5.5=19.5 $$

Question 3

Solve the equation

$$ 20:4x=5 $$

Another example

$Z + 7 = 15$

First let's see that this time the variable is $Z$ . The variable can be denoted by any letter we want.

As we have explained before, we are interested in finding the value of the $Z$ that will give us the solution to the equation. Therefore, we will now try to isolate $Z$ . We will do this by subtracting $7$ from the two members of the equation.

It looks like this:

$Z + 7 = 15$

We will obtain:

$Z + 7 -7 = 15 – 7$

$Z = 8$

This is the solution of the equation. Again, it is always convenient to check if we have found the correct value of the unknown by placing our answer in the original equation.

Let's remember what the original equation was:

$Z + 7 = 15$

let's put

$Z = 8$

and we will get:

$8 + 7 = 15$

$15=15$

This really is a true statement, i.e., the answer we received is correct.

Solving equations by applying multiplication and division operations

So far we have solved equations by applying addition and subtraction operations to both sides of the equation. Now we will see other examples of equations that we will solve with multiplication and division operations:

Do you know what the answer is?

Question 1

Solve the equation

$8x\cdot10=80$

Question 2

$$ 5x=0 $$

Question 3

$$ 5x=1 $$

What is the value of x?

Exercise 1

Find the value of the unknown in the following equation and check that it is correct.

$2X = 8$

We want to isolate the $X$ . We divide both members of the equation by $2$ . We will write it like this:

$2X/2= 8/2$

and we will get :

$X = 4$

Also in this case it is convenient to place the solution in the original equation to see if we have done it right:

$2\times 4 = 8$

$8 = 8$

We obtained a correct result, that is, our solution is right.

Exercise 2

Find the value of the unknown in the following equation and check that it is correct.

$-3Y = 18$

To isolate the variable Y we divide both members of the equation by $-3$

$-3Y/-3 = 18/-3$

$Y = -6$

To verify our result, it is always convenient to place it in the original equation. Try it!

Check your understanding

Question 1

Find the value of the parameter X:

$$ x+5=8 $$

Question 2

Solve for X:

$$ 3+x=4 $$

Question 3

Solve for X:

$$ 5-x=4 $$

Exercise 3

Find the value of the unknown in the following equation and check that it is correct.

$\frac{1}{3}x=5$

Here we have a fraction in the equation. We want to get rid of it and isolate the $X$ . We multiply both members of the equation by. $3$

$3\times\frac{1}{3}x=3\times5$

We will obtain:

$x=15$

To verify this we will place the result obtained in the original equation:

$\frac{1}{3}\times 15=5$

$5=5$

That is, the result obtained is correct.

Exercise 4

Find the value of the unknown in the following equation and check that it is correct.

$2x + 3 = 5$

This exercise requires subtracting and dividing operations. First, we subtract $3$ from the two members of the equation:

$2x + 3 = 5$

$2x + 3 - 3 = 5 – 3$

$2x = 2$

Now we will divide the two members of the equation by. $2$ and we obtain:

$2x/2 = 2/2$

$X = 1$

Let's place the result obtained in the original equation to check if we have done it right:

$2\times 1 + 3 = 5$

$5 = 5$

That is, the result obtained is correct.

Do you think you will be able to solve it?

Question 1

Solve for X:

$$ -8-x=-5 $$

Question 2

Find the value of the parameter X

$$ -8-x=5 $$

Question 3

Solve for X:

$$ -5+x=-3 $$

Exercise 5

Find the value of the unknown in the following equation and check that it is correct.

$X-6=0$

This exercise requires the operation of adding $6$ in both members of the equation, so we have:
$X-6+6=0+6$

Simplifying we obtain that the solution of the equation is $X=6$ since if we put $6$ instead of the $X$ we will obtain the result $0$ on both sides of the equation, we will have two equivalent members.

Exercise 6

Find the value of the unknown in the following equation and check that it is correct.

$2X-6=0$

This exercise requires the operation of adding $6$ in both members of the equation, so we have:

$2X-6+6=0+6$

$2X=6$

Now we divide by $2$ both sides of the equation :

$2X/2=6/2$

$X=3$

The solution of the equation is $X=3$ because if we put $3$ instead of the $X$ we will get the result $0$ on both sides of the equation, we will have two equivalent members.

Test your knowledge

Question 1

Solve for X:

$$ 5x=25 $$

Question 2

Solve for X:

$$ 6x=72 $$

Question 3

Solve the equation

$$ 5x-15=30 $$

Exercise 7

Find the value of the unknown in the following equation and check that it is correct.

$3X-5=16$

This exercise requires the operation of adding $5$ in both members of the equation, so we have:

$3X-5+5=16+5$

$3X=21$

Now we divide by $3$ both sides of the equation:

$3X/3=21/3$

$X=7$

The solution of the equation is $X=7$ since if we put $7$ instead of the $X$ we will get the result $16$ on both sides of the equation, we will have two equivalent members.

Questions on the subject

How to clear an unknown?

Isolating the variable with mathematical operations.

Do you know what the answer is?

Question 1

$$ 4x:30=2 $$

Question 2

Solve the equation

$$ 7x+5.5=19.5 $$

Question 3

Solve the equation

$$ 20:4x=5 $$

How to isolate a variable or unknown?

Passing like terms to each side of the equality and performing mathematical operations.

How to corroborate the solution of an equation?

Substituting the value found in the original equation and check that the equality is satisfied.

Check your understanding

Question 1

Solve the equation

$8x\cdot10=80$

Question 2

$$ 5x=0 $$

Question 3

$$ 5x=1 $$

What is the value of x?

What is an unknown?

It is the unknown value of the equation.

How to solve a first order equation with one unknown?

Isolating the variable with mathematical operations.

Do you think you will be able to solve it?

Question 1

Find the value of the parameter X:

$$ x+5=8 $$

Question 2

Solve for X:

$$ 3+x=4 $$

Question 3

Solve for X:

$$ 5-x=4 $$

What is a first order equation with one unknown?

It is a mathematical equality involving a variable raised to the first power and fixed values that are numbers.

If this article interested you, you may also be interested in the following articles:

In the Tutorela Math Blog you will find a wide variety of articles about mathematics.

Test your knowledge

Question 1

Solve for X:

$$ -8-x=-5 $$

Question 2

Find the value of the parameter X

$$ -8-x=5 $$

Question 3

Solve for X:

$$ -5+x=-3 $$

Examples with solutions for Linear Equations

Exercise #1

Solve the equation

$5x-15=30$

Video Solution

Step-by-Step Solution

We start by moving the sections:

5X-15 = 30
5X = 30+15

5X = 45

Now we divide by 5

X = 9

Answer

$x=9$

Exercise #2

Solve the equation

$20:4x=5$

Video Solution

Step-by-Step Solution

To solve the exercise, we first rewrite the entire division as a fraction:

$\frac{20}{4x}=5$

Actually, we didn't have to do this step, but it's more convenient for the rest of the process.

To get rid of the fraction, we multiply both sides of the equation by the denominator, 4X.

20=5*4X

20=20X

Now we can reduce both sides of the equation by 20 and we will arrive at the result of:

X=1

Answer

$x=1$

Exercise #3

Find the value of the parameter X

$\frac{1}{3}x+\frac{5}{6}=-\frac{1}{6}$

Video Solution

Step-by-Step Solution

First, we will arrange the equation so that we have variables on one side and numbers on the other side.

Therefore, we will move $\frac{5}{6}$ to the other side, and we will get

$\frac{1}{3}x=-\frac{1}{6}-\frac{5}{6}$

Note that the two fractions on the right side share the same denominator, so you can subtract them:

$\frac{1}{3}x=-\frac{6}{6}$

Observe the minus sign on the right side!

$\frac{1}{3}x=-1$

Now, we will try to get rid of the denominator, we will do this by multiplying the entire exercise by the denominator (that is, all terms on both sides of the equation):

$1x=-3$

$x=-3$

Answer

-3

Exercise #4

Solve the equation

$4\frac{1}{3}\cdot x=21\frac{2}{3}$

Video Solution

Step-by-Step Solution

We have an equation with a variable.

Usually, in these equations, we will be asked to find the value of the missing (X),

This is how we solve it:

To solve the exercise, first we have to change the mixed fractions to an improper fraction,

So that it will then be easier for us to solve them.

Let's start with the four and the third:

To convert a mixed fraction, we start by multiplying the whole number by the denominator

4*3=12

Now we add this to the existing numerator.

12+1=13

And we find that the first fraction is 13/3

Let's continue with the second fraction and do the same in it:
21*3=63

63+2=65

The second fraction is 65/3

We replace the new fractions we found in the equation:

13/3x = 65/3

At this point, we will notice that all the fractions in the exercise share the same denominator, 3.

Therefore, we can multiply the entire equation by 3.

13x=65

Now we want to isolate the unknown, the x.

Therefore, we divide both sides of the equation by the unknown coefficient -
13.

63:13=5

x=5

Answer

$x=5$

Exercise #5

The area of the rectangle below is equal to 22x.

Calculate x.

Video Solution

Step-by-Step Solution

The area of the rectangle is equal to the length multiplied by the width.

Let's list the known data:

$22x=\frac{1}{2}x\times(x+8)$

$22x=\frac{1}{2}x^2+\frac{1}{2}x8$

$22x=\frac{1}{2}x^2+4x$

$0=\frac{1}{2}x^2+4x-22x$

$0=\frac{1}{2}x^2-18x$

$0=\frac{1}{2}x(x-36)$

For the equation to be equal, x needs to be equal to 36

Answer

$x=36$

Start practice