The area of the kite can be calculated by multiplying the lengths of the diagonals and dividing this product by .
Area of a Kite Practice Problems and Solutions Online
Master kite area calculations with step-by-step practice problems. Learn convex and concave deltoid formulas, diagonal properties, and solve real geometry exercises.
- Calculate kite area using diagonal multiplication formula A = (d₁ × d₂)/2
- Identify and work with convex and concave deltoid properties
- Apply diagonal bisector properties to solve reverse calculation problems
- Distinguish between main and secondary diagonals in kite geometry
- Solve multi-step problems involving kite area and diagonal lengths
- Practice with real exam-style quadrilateral geometry questions
Understanding Area of a Deltoid
How do we calculate the area of a kite?
Deltoid Area Formula
To facilitate the understanding of the concept of calculus, you can use the following drawing and the accompanying formula:
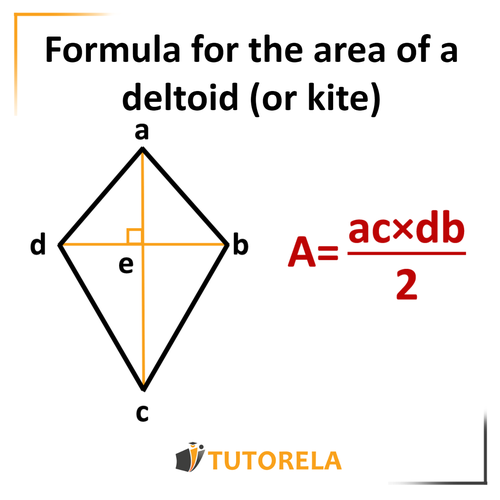
Practice Area of a Deltoid
ACBD is a deltoid.
AD = AB
CA = CB
Given in cm:
AB = 6
CD = 10
Calculate the area of the deltoid.
Examples with solutions for Area of a Deltoid
ABDC is a deltoid.
AB = BD
DC = CA
AD = 12 cm
CB = 16 cm
Calculate the area of the deltoid.
First, let's recall the formula for the area of a rhombus:
(Diagonal 1 * Diagonal 2) divided by 2
Now we will substitute the known data into the formula, giving us the answer:
(12*16)/2
192/2=
96
Answer:
96 cm²
Shown below is the deltoid ABCD.
The diagonal AC is 8 cm long.
The area of the deltoid is 32 cm².
Calculate the diagonal DB.
First, we recall the formula for the area of a kite: multiply the lengths of the diagonals by each other and divide the product by 2.
We substitute the known data into the formula:
We reduce the 8 and the 2:
Divide by 4
Answer:
8 cm
Indicate the correct answer
The next quadrilateral is:
Initially, let us examine the basic properties of a deltoid (or kite):
A quadrilateral is classified as a deltoid if:
- It has two distinct pairs of adjacent sides that are equal in length.
In the question's image, we observe the following:
- There are lines connecting A to B, B to C, C to D, and D to A, suggesting a typical quadrilateral.
- The shape, given its central symmetry (as it is formed by joining these particular points which extend equal lines), is reminiscent of a symmetric or bilaterally mirrored formation.
- Given the symmetry, it suggests all internal angles are less than 180 degrees, confirming the figure as a convex shape.
From this analysis, the quadrilateral satisfies the characteristic of having pairs of equal adjacent sides which confirms it as a deltoid. The symmetry suggests it is not concave (which occurs when at least one interior angle is greater than 180 degrees).
Therefore, the given quadrilateral, based on its properties and symmetry, is a convex deltoid.
Answer:
Convex deltoid
Look at the deltoid in the figure:
What is its area?
Let's begin by reminding ourselves of the formula for the area of a kite
Both these values are given to us in the figure thus we can insert them directly into the formula:
(4*7)/2
28/2
14
Answer:
14
Indicate the correct answer
The next quadrilateral is:
The problem requires determining if a given quadrilateral is a deltoid, and if so, whether it is convex, concave, or indeterminate based on the provided diagram. A deltoid, or kite, is generally defined as a quadrilateral with two pairs of adjacent sides being of equal length. Thus, a visual analysis is essential here as only diagrammatic data is available.
To address this, one must closely analyze the properties of the given quadrilateral in terms of similarity and its symmetry relative to a conventional deltoid structure:
- Typically, you'd look for simultaneous symmetry or patterns indicating two equal-length adjacent pairs of sides.
- After examining the diagram and the naming convention (vertices labelled A, B, C, D), see if it implies any such congruency visually or through label symmetry.
- Lack of distinct clues for equal side pairs or diagonals prevents concluding its specific nature without additional information, especially since no specific length measures or angles are provided.
Given this and under diagram-only conditions, it's not possible to definitively prove that the shape is completely a deltoid (convex or concave). Therefore, without further data, identifying the indicated quadrilateral deltoid nature is beyond determining from the given data itself.
Consequently, the correct answer is: It is not possible to prove if it is a deltoid or not.
Answer:
It is not possible to prove if it is a deltoid or not